- Related AI/ML Methods: Dimension Reduction Principal Component Analysis
- Related Traditional Methods: Factor Analysis, Principal Component Analysis
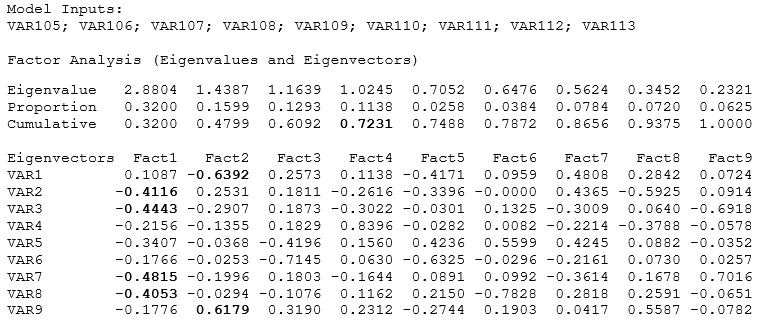
This method runs Factor Analysis to analyze interrelationships within large numbers of variables and simplifies said factors into a smaller number of common factors. The method condenses information contained in the original set of variables into a smaller set of implicit factor variables with minimal loss of information. The analysis is related to Principal Component Analysis (PCA) by using the correlation matrix and applying PCA coupled with a Varimax matrix rotation to simplify the factors. The same results interpretation is used for Factor Analysis as for PCA. For instance, Figure 9.66 illustrates an example where we start with 9 independent variables that are unlikely to be independent of one another, such that changing the value of one variable will change another variable. Factor analysis helps identify and eventually replace the original independent variables with a new set of fewer variables that are less than the original but are uncorrelated to one another, while, at the same time, each of these new variables is a linear combination of the original variables. This means most of the variation can be accounted for by using fewer explanatory variables. Factor analysis is therefore used to analyze interrelationships within large numbers of variables and simplifies said factors into a smaller number of common factors. The method condenses information contained in the original set of variables into a smaller set of implicit factor variables with minimal loss of information.
The data input requirement is simply the list of variables you want to analyze (separated by semicolons for individual variables or separated by a colon for a contiguous set of variables, such as VAR105:VAR113 for all 9 variables).

Figure 9.66: AI/ML Dimension Reduction Factor Analysis (Unsupervised)
We started with 9 independent variables, which means the factor analysis results will return a 9×9 matrix of eigenvectors and 9 eigenvalues. Typically, we are only interested in components with eigenvalues >1. Hence, in the results, we are only interested in the first four factors or components. Notice that the first four factors (the first four result columns) return a cumulative proportion of 72.31%. This means that using these four factors will explain 72.31% of the variation in all the independent factors themselves. Next, we look at the absolute values of the eigenvalue matrix. It seems that variables 2, 3, 7, 8 can be combined into a new variable in factor 1, with variables 1 and 9 as the second factor, and so forth.