File Name: Credit Analysis – Credit Premium
Location: Modeling Toolkit | Credit Analysis | Credit Premium
Brief Description: Determines the credit risk premium that should be charged beyond any standard interest rates depending on the default probability of the debt holder
Requirements: Modeling Toolkit
This model is used to determine the credit risk premium that should be charged above the standard interest rate given the default probability of this debt’s or credit’s anticipated cash flows. Enter the years and relevant cash flows in the model as well as the interest rate and anticipated default probability and click Compute to determine the credit spread required (Figure 10.1). All values should be positive, and the default probability input can be determined using any of the Modeling Toolkit’s default probability models.
For instance, in Figure 10.1, assume a regular 10-year bond with a $1,000 face value paying a 10% coupon rate. Where the prevailing interest rate is 5%, a 1% default probability means that the default risk premium spread is 0.14%, making the total interest charge 5.14%.
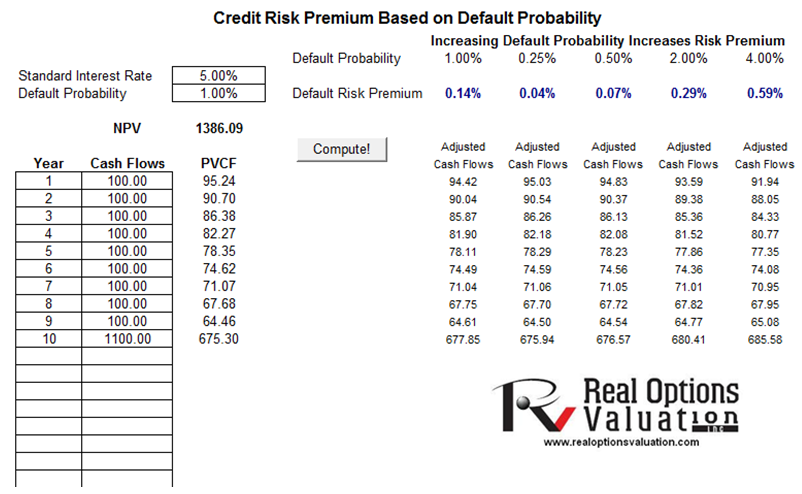
Figure 10.1: A simple credit spread premium computation given default probabilities
The present value of cash flows (PVCF) is the present value of future coupon payments and face value receipt at maturity, discounted at the prevailing interest rate. The sum of these values is the net present value (NPV), which is the price of the bond assuming zero default. By adding a probability of default, the cash flows are adjusted by this default rate and a corresponding default risk premium can be determined whereby the NPV of these risk-adjusted PVCF values will equal the original no-default NPV.
The results indicate that the lower the probability of default on this debt, the lower the additional default spread (interest rate premium), and the higher the probability of default, the higher the required interest rate premium. Using this simple probability-adjusted cash flow model, we can determine the approximate simple credit spread required to obtain the same probability-adjusted cash flow as another debt with no default. This is a simple cash flow model for approximation purposes and does not account for more exotic and real-life conditions such as mean-reverting interest rates, stochastic interest rates (smiles, frowns, and other shapes with localized time-dependent volatilities), credit risk migration, risk-neutral versus empirical probabilities of default adjustments, recovery rate, changing cumulative probabilities of default, and other qualitative factors, which are addressed in later chapters and models. Nonetheless, this model provides a simple and highly intuitive approximation of the default spread required on a risky debt or credit issue and can use used as a simple benchmark against more advanced models that are discussed in later chapters.

