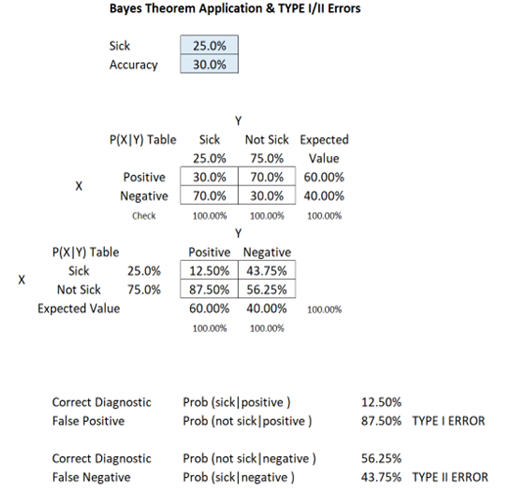
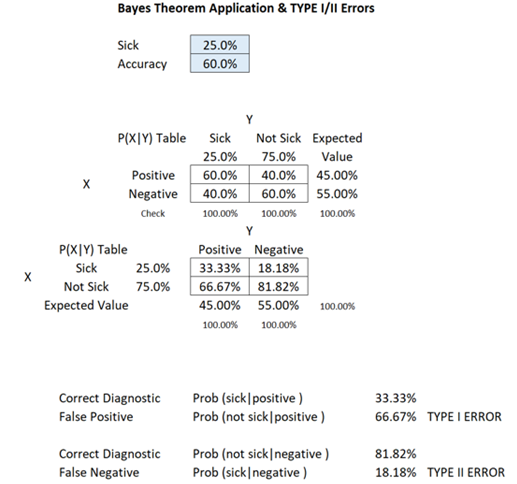
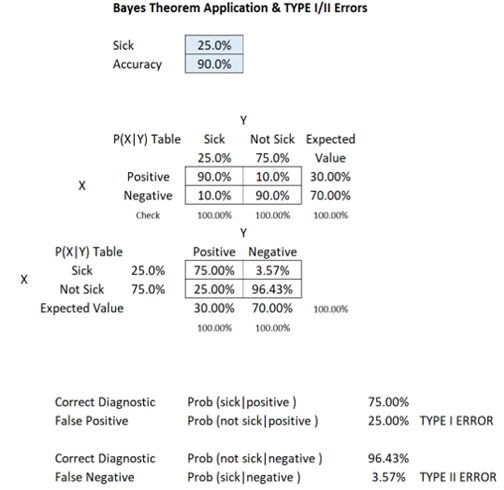
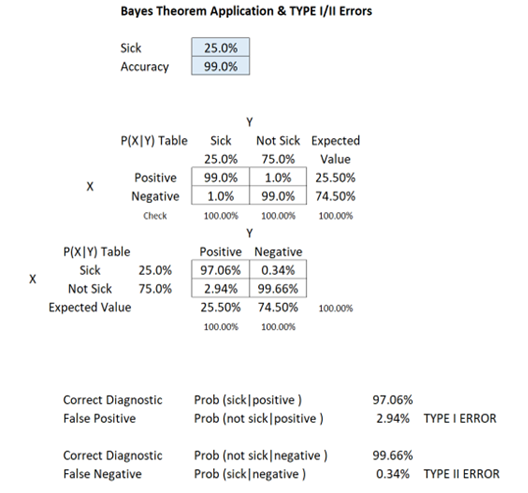
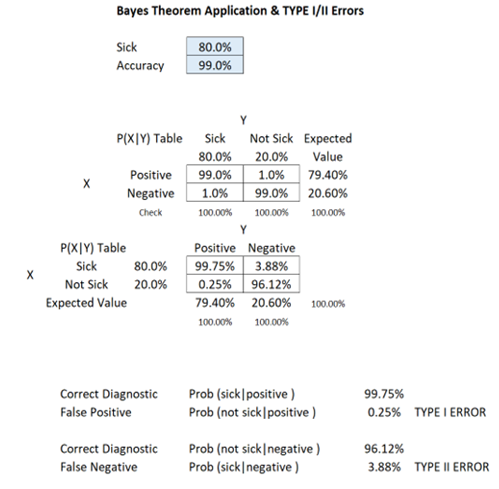
COVID-19 is highly contagious and at one point, 25% of the population has been infected. Suppose there is a low-priced rapid test kit that claims to have 99% accuracy in detecting the COVID-19 virus without PCR. Accuracy in this case means that if a person is truly sick, the test returns a positive result. However, the kit also has a possibility of false positives, creating mistakes in diagnosing healthy persons and identifying them as sick (i.e., the test shows a positive result even if the person is really not sick or infected). In the case of a person being tested with this kit shows a positive result, what is the probability that the person is really sick or infected, or shows negative when the person is, in fact, not sick or infected (correct diagnosis)? What is the probability of false positives and false negatives (incorrect diagnosis)? Is Type I or Type II error a bigger problem in this case?
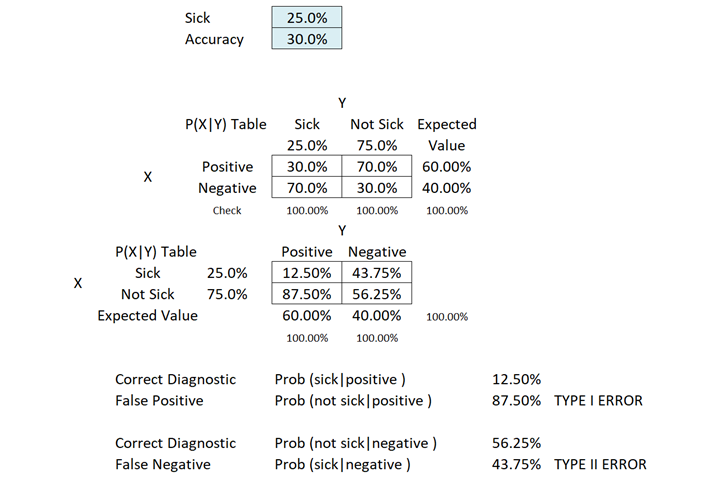
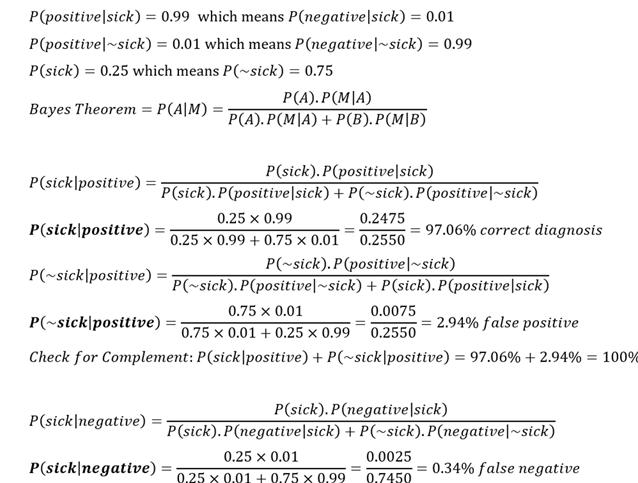
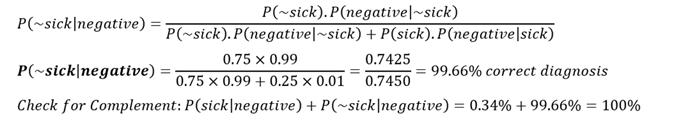
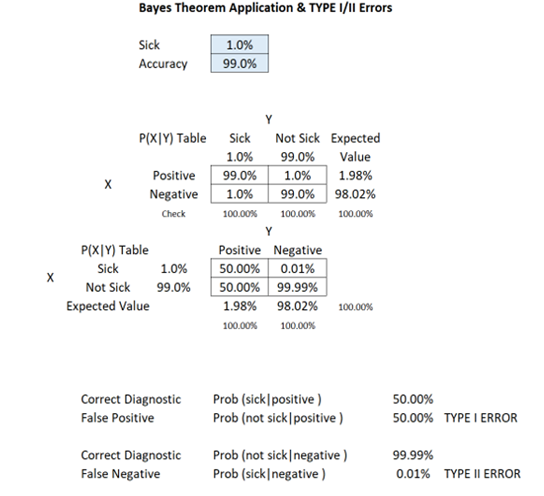
An interesting phenomenon occurs in this case. Rare diseases (low population with the sickness) even with higher levels of test accuracy tend to create a higher probability of false positives, but the false negatives are still relatively low. This is why it is so hard to diagnose exotic and uncommon illnesses. With a regular percentage of the population infected and sick (e.g., 25%), a lower accuracy test will yield significantly high false positives and false negatives. However, false positives usually outweigh false negatives in this situation.
![]()
![]()