File Names: Personal Finance (multiple models and examples in Modeling Toolkit)
Location: Modeling Toolkit | Personal Finance (multiple models)
Brief Description: Shows some of the personal finance models that exist in Modeling Toolkit (not all of the 30 models are shown)
Requirements: Modeling Toolkit and Risk Simulator
This chapter reviews several personal finance models, starting with a retirement savings growth model and modeling of sufficiency in retirement funds, to an analysis of whether you should buy or rent your home, saving and investing for your child’s college, and accelerated amortization of home mortgages.
Retirement Savings Growth
If you participate in a 401(k) program or a similar retirement savings account, and your employer contributes or has some matching funds, how much money will you have saved by the time you intend to retire? Use this quick 401(k) model (Figure 111.1) to determine the amount you will have at retirement. This model also shows you the difference between a taxable versus a nontaxable investment. Clearly, the model assumes that the economic and financial conditions remain stable over time, and for more detailed analysis, please see a certified financial analysts or financial planner. Nonetheless, this model helps you gauge how much you will have saved by retirement. If you wish to also include the payouts during retirement, please see the next section (Retirement Funding with Inflation Adjustment model) for more details. Finally, you can also model a stochastic or dynamic interest rate of return environment by setting Risk Simulator assumptions and running Monte Carlo simulations.
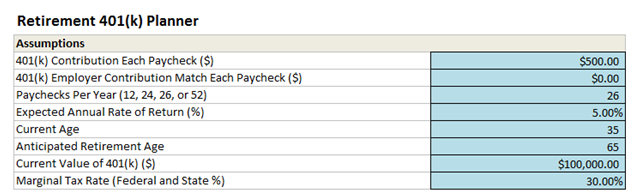
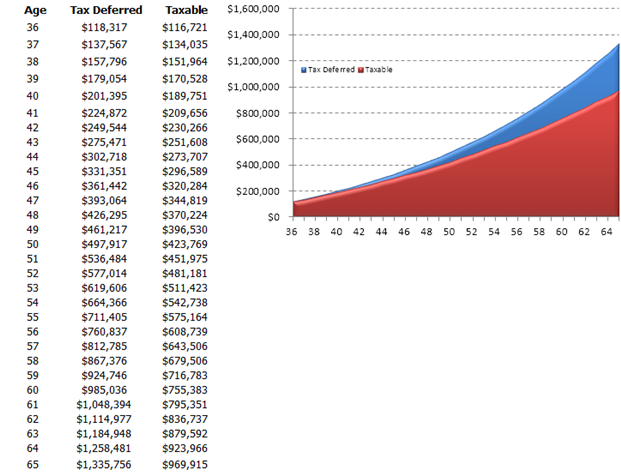
Figure 111.1: Retirement planning model
Retirement Funding with Inflation Adjustment
How soon do you need to start saving for your retirement? The short answer is that the sooner, the better! The earlier you start saving, the less monthly savings you will need to contribute towards your retirement fund. In this model (Figure 111.2), we look at your current salary and accounting for the inflation rate between now and the end of your natural life, and some investment returns on your savings, we can determine the minimum amount to save per year for retirement. The desired ending value of this retirement fund can also be set, using a value of $0 if you intend to exhaust the fund, or some positive value if you wish to provide a buffer amount in case inflation rises higher than expected, or to provide the family some lump sum amount to cover any unforeseen expenses. This model is built to intentionally not include any additional government-sponsored programs (e.g., Social Security, Welfare) because different countries have different rules, regulations, and plans. Also, you can consider these plans as additional benefits above and beyond your retirement savings here. Note that the model screenshot intentionally has some hidden rows to conserve space.

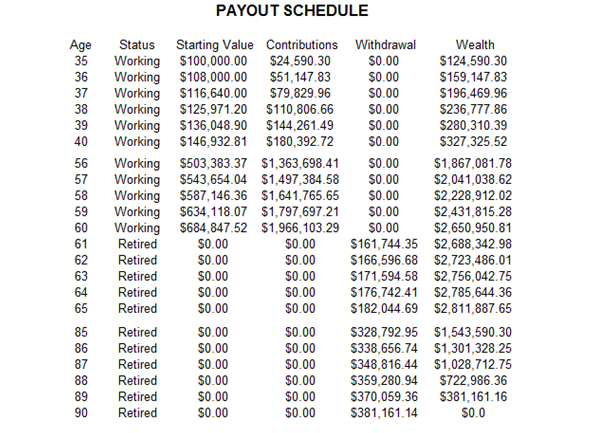
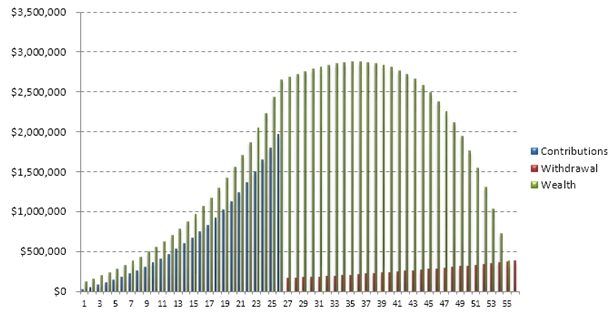
Figure 111.2: Retirement analysis
Buying versus Renting Your Home
Is it better to buy your home or to rent? Well, it really depends on what type of house you are purchasing, the maintenance cost, rental price, down payment required for the house, the mortgage you will incur, whether you are retired empty nesters or just starting your career, and many other issues. This Buy versus Rent model (Figure 111.3) helps you make this determination quickly to see if it is indeed more financially profitable buying versus renting your home. We will leave the other psychological factors up to you!
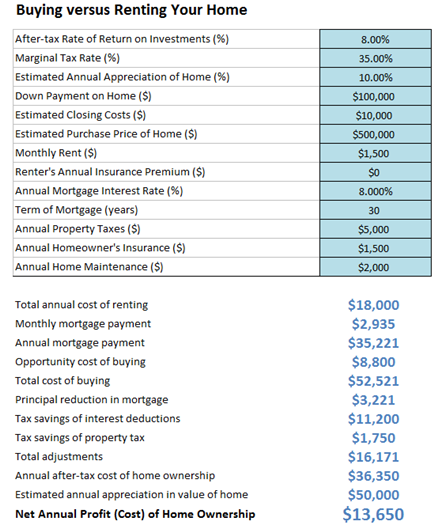
Figure 111.3: Buy versus rent
College Funding with Inflation Adjustment
How much money do you need to start saving for your child’s college education? Well, as usual, the answer is always the sooner, the better! The earlier you start saving, the less monthly savings you will need to contribute towards that college fund. In this College Funding model (Figure 111.4), we look at what the current cost of attending college per year is, accounting for the inflation rate between now and the end of the college education, and some investment returns on your savings. You can also set the desired ending value of this college fund, using a value of $0 if you intend to only pay for the education, or some positive value, if you wish to provide a cost buffer in case prices, rise higher than expected, or to provide the fresh graduate some lump sum amount when s/he graduates (a nice car or apartment down payment, moving expenses, etc.).
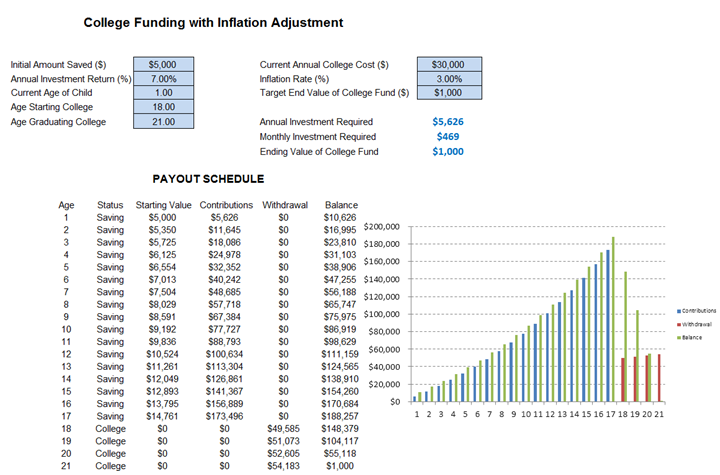
Figure 111.4: Saving for your child’s college education
Mortgage Amortization and Accelerated Payoff
You frequently hear about biweekly mortgage payments, or friends say that you should put a little extra into your loan or mortgage to speed up the payoff on your home. This Mortgage Accelerated Payoff model (Figure 111.5) shows you how much time and how much interest you will be saving if you put some extra money into paying off the mortgage every month.
In an amortization schedule, you notice that the monthly payments are identical such that the remaining balance ends up as zero at the end of the mortgage life. Notice also that the principal paid per month increases and interest paid decreases over the life of the mortgage. This is because the monthly mortgage payment goes toward paying off the principal and interest on the remaining principal. Over time, as the principal of the mortgage is reduced, the interest on the remaining principal decreases. So, with the same monthly payment, a larger portion of the payment goes towards paying down the principal and less towards the interest.
Notice that by paying a little extra each month, you can drastically reduce the total interest you actually pay throughout the life of the mortgage and cut years from the life of the mortgage! Note that the model screenshot intentionally has some hidden rows to conserve space.
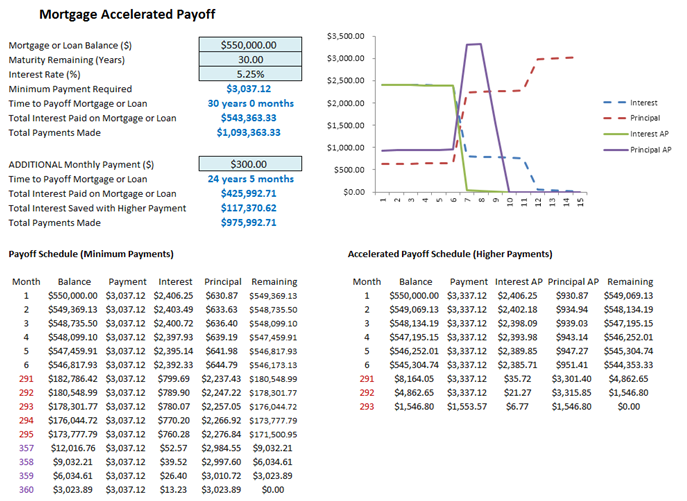
Figure 111.5: Mortgage accelerated payoff model

