File Name: Exotic Options – American Call Option on Index Futures
Location: Modeling Toolkit | Real Options Models | American Call Option on Index Futures
Brief Description: Computes the value of an Index option using closed-form models and binomial lattices
Requirements: Modeling Toolkit, Real Options SLS
The Index Option is similar to a regular option but the underlying asset is a reference stock index such as the Standard & Poor’s 500. The analysis can also be solved using a closed-form Generalized Black-Scholes-Merton model. The model used in this chapter is similar to the closed-form model but applies the binomial lattice instead. The difference here is that Black-Scholes can solve only European options while the binomial lattice model is capable of solving American, European, and Bermudan or mixed and customized options. Instead of using the asset value or current stock price as the input, we use the current Index value. All other inputs remain the same, as in other options models (see Figure 33.1). Index futures are an important investment vehicle as stock indexes cannot be traded directly, so futures based on stock indexes are the primary vehicles for trading indexes. Index futures operate in essentially the same way as other futures and are traded in the same way. As indexes are based on many separate stocks, index futures are settled in cash rather than stocks. In addition, index futures allow investors to participate in the entire market without the significant cost of purchasing each underlying stock in an index. Index futures are widely used for hedging market movements and applied in portfolios for their diversification effects.
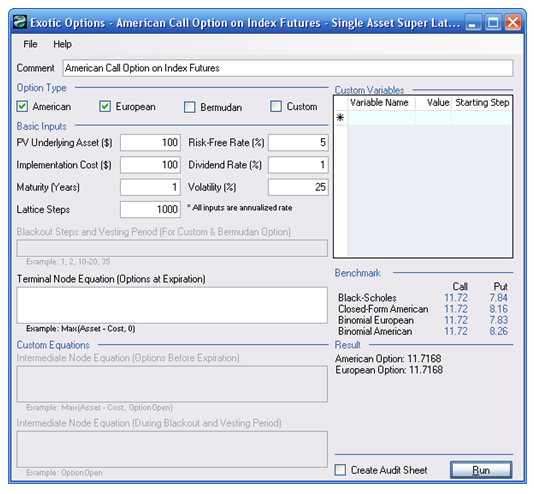
Figure 33.1: American and European index futures

