The correlation coefficient is a measure of the strength and direction of the relationship between two variables, and it can take on any values between –1.0 and +1.0. That is, the correlation coefficient can be decomposed into its sign (positive or negative relationship between two variables) and the magnitude or strength of the relationship (the higher the absolute value of the correlation coefficient, the stronger the relationship). The correlation coefficient can be computed in several ways. The first approach is to manually compute the correlation r of two variables x and y using:
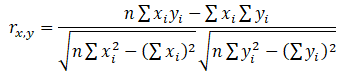
The second approach is to use Excel’s CORREL function. For instance, if the 10 data points for x and y are listed in cells A1:B10, then the Excel function to use is CORREL (A1:A10, B1:B10).
The third approach is to run Risk Simulator’s Analytical Tools | Distributional Fitting | Multi-Variable, and the resulting correlation matrix will be computed and displayed.
It is important to note that correlation does not imply causation. Two completely unrelated random variables might display some correlation, but this does not imply any causation between the two (e.g., sunspot activity and events in the stock market are correlated, but there is no causation between the two).
There are two general types of correlations: parametric and nonparametric correlations. Pearson’s product moment correlation coefficient is the most common correlation measure and is usually referred to simply as the correlation coefficient. However, Pearson’s correlation is a parametric measure, which means that it requires both correlated variables to have an underlying normal distribution and that the relationship between the variables is linear. When these conditions are violated, which is often the case in Monte Carlo simulation, the nonparametric counterparts become more important. Spearman’s rank correlation and Kendall’s tau are the two nonparametric alternatives. The Spearman correlation is most commonly used and is most appropriate when applied in the context of Monte Carlo simulation—there is no dependence on normal distributions or linearity, meaning that correlations between different variables with different distributions can be applied. In order to compute the Spearman correlation, first rank all the and variable values and then apply the Pearson’s correlation computation. In contrast, Kendall’s Tau is a nonparametric correlation coefficient, considering concordance or discordance, based on all possible pairwise combinations of ordinal ranked data. The null hypothesis tested is that there is zero correlation between the two variables. BizStats supports the Kendall’s Tau calculation with ties and without ties.
Figure 9.29 provides some visual examples of pairwise correlations between X and Y. Positive correlations (A and D) can be visualized as positive slopes, whereas negative correlations are negatively sloped (B). A flat line denotes zero correlation. The closer the values are to a linear line, the higher the absolute value of the correlation or |C|>|B|>|A|. The charts A–D indicate linear correlations whereas E and G show that nonlinear correlations are better fits than linear correlations F and H.
In the case of Risk Simulator, the correlation used is the more robust nonparametric Spearman’s rank correlation. However, to simplify the simulation process, and to be consistent with Excel’s correlation function, the correlation inputs required are the Pearson’s correlation coefficient. Risk Simulator will then apply its own algorithms to convert them into Spearman’s rank correlation, thereby simplifying the process. Additionally, to simplify the user interface, we allow users to enter the more common Pearson’s product-moment correlation (e.g., computed using Excel’s CORREL function), while in the mathematical codes, we convert these correlations into Spearman’s rank-based correlations for distributional simulations.
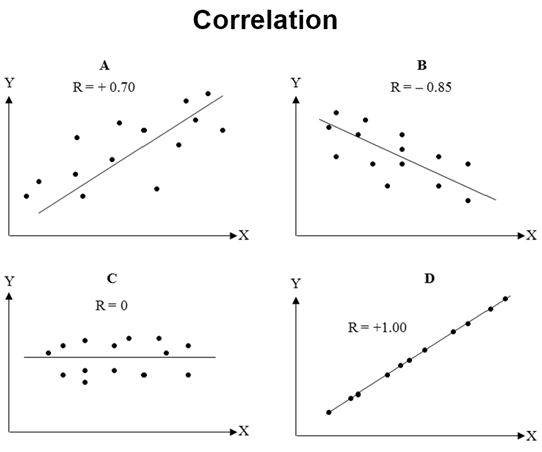
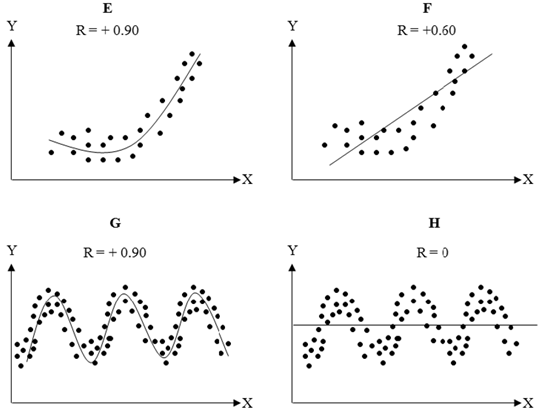
Figure 9.29: Linear and Nonlinear Correlations
The following lists some key correlation effects and details that will be helpful in modeling:
- Correlation coefficients range from –1.00 to + 1.00, with 0.00 as a possible value.
- The correlation coefficient has two parts: a sign and a value. The sign shows the directional relationship whereas the value shows the magnitude of the effect (the higher the value, the higher the magnitude, while zero values imply no relationship). Another way to think of a correlation’s magnitude is the inverse of noise (the lower the value, the higher the noise).
- Correlation implies dependence and not causality. In other words, if two variables are correlated, it simply means both variables move together in the same or opposite direction (positive versus negative correlations) with some strength of co-movements. It does not, however, imply that one variable causes another. In addition, one cannot determine the exact impact or how much one variable causes another to move.
- If two variables are independent of one another, the correlation will be, by definition, zero. However, a zero correlation may not imply independence (because there might be some nonlinear relationships).
- Correlations can be visually approximated on an X-Y If we generate an X-Y plot and the line is flat, the correlation is close to or equal to zero; if the slope is positive (data slopes upward), then the correlation is positive; if the slope is negative (data slopes downward), then the correlation is negative; the closer the scatter plot’s data points are to a straight line, the higher the linear correlation value.
- The population correlation coefficient ρ can be defined as the standardized covariance:
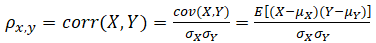 where X and Y are the data from two variables’ population. The covariance measures the average or expectation (E) of the co-movements of all X values from its mean (μx) multiplied by the co-movements of all Y values from its population mean (μy). The value of covariance is between negative and positive infinity, making its interpretation fairly difficult. However, standardizing the covariance by dividing it by the population standard deviation (σ) of X and Y, we obtain the correlation coefficient, which is bounded between –1.00 and +1.00.
where X and Y are the data from two variables’ population. The covariance measures the average or expectation (E) of the co-movements of all X values from its mean (μx) multiplied by the co-movements of all Y values from its population mean (μy). The value of covariance is between negative and positive infinity, making its interpretation fairly difficult. However, standardizing the covariance by dividing it by the population standard deviation (σ) of X and Y, we obtain the correlation coefficient, which is bounded between –1.00 and +1.00.
- However, in practice, we typically only have access to sample data and the sample correlation coefficient (r) can be determined using the sample data from two variables x and y, their averages (x̅ and ȳ ), their standard deviations (sx,sy), and the count (n) of x and y data pairs:
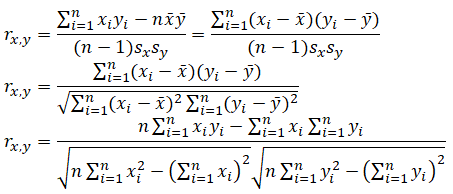
- Correlations are symmetrical. In other words, the rA,B = rB,A. Therefore, we sometimes call correlation coefficients pairwise correlations.
- If there are n variables, the number of total pairwise correlations is
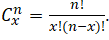 For example, if there are n = 3 variables, A, B, C, the number of pairwise (x = 2, or two items are chosen at a time) combinations total
For example, if there are n = 3 variables, A, B, C, the number of pairwise (x = 2, or two items are chosen at a time) combinations total 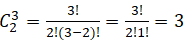 correlation pairs: rA,B , rA,C and rB,C.
correlation pairs: rA,B , rA,C and rB,C. - Correlations can be linear or nonlinear. Pearson’s product-moment correlation coefficient is used to model linear correlations, and Spearman’s rank-based correlation is used to model nonlinear correlations.
- Linear correlations(also known as Pearson’s R) can be computed using Excel’s CORREL function or using the equations described previously.
- Nonlinear correlations are computed by first ranking the nonlinear raw data, and then applying the linear Pearson’s correlation. The result is a nonlinear rank correlation or Spearman’s R. Use the correlation version (linear or nonlinear) that has a higher absolute value.
- Pearson’s linear correlation is also a parametric correlation, with the implicit underlying assumption that the data is linear and close to being normally distributed. Spearman’s rank correlation is nonparametric and has no dependence on the underlying data being normal.
- The square of the correlation coefficient (R) is called the coefficient of determination or R-squared. This is the same R-squared used in regression modeling, and it indicates the percentage variation in the dependent variable that is explained given the variation in the independent variable(s).
- R-squared is limited to being between 0.00 and 1.00, and is usually shown as a percentage. Specifically, as R has a domain between –1.00 and +1.00, squaring either a positive or negative R value will always yield a positive R-squared value, and squaring any R value between 0.00 and 1.00 will always yield an R-squared result between 0.00 and 1.00. This means that R-squared is localized to between 0% and 100% by construction.
- In a simple positively related model, negative correlations reduce total portfolio risk, whereas positive correlations increase total portfolio risk. Conversely, in a simple negatively related model, negative correlations increase total portfolio risk, whereas positive correlations decrease total portfolio risk.
-
- Positive Model (+) with Positive Correlation (+) = Higher Risk(+).
- Positive Model (+) with Negative Correlation (–) = Lower Risk(–).
- Negative Model (–) with Positive Correlation (+) = Lower Risk(–).
- Negative Model (–) with Negative Correlation (–) = Higher Risk(+).
- Portfolio Diversification typically implies the following condition: Positive Model (+) with Negative Correlation (–) = Lower Risk (–). For example, the portfolio level’s (p) diversifiable risk is
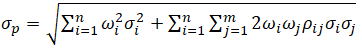 where ωi,j are the respective weights or capital allocation across each project; pi,j are the respective cross-correlations between the assets, and σi,j are the volatility Hence, if the cross-correlations are negative, there are risk diversification effects, and the portfolio risk decreases.
where ωi,j are the respective weights or capital allocation across each project; pi,j are the respective cross-correlations between the assets, and σi,j are the volatility Hence, if the cross-correlations are negative, there are risk diversification effects, and the portfolio risk decreases.
- Examples of a simple positively related model are an investment portfolio (the total of the returns in a portfolio is the sum of each individual asset’s returns, i.e., A + B + C = D, therefore, increase A or B or C, and the resulting D will increase as well, indicating a positive directional relationship) or the total of the revenues of a company is the sum of all the individual products’ revenues. Negative correlations in such models mean that if one asset’s returns decrease (losses), another asset’s returns would increase (profits). The spread or distribution of the total net returns for the entire portfolio would decrease (lower risk). The negative correlation would, therefore, diversify the portfolio risk.
- Alternatively, an example of a simple negatively related model is revenue minus cost equals net income (i.e., A – B = C, which means that as B increases, C would decrease, indicating a negative relationship). Negatively correlated variables in such a model would increase the total spread of the net income distribution.
- In more complex or larger models where the relationship is difficult to determine (e.g., in a discounted cash flow model where we have revenues of one product being added to revenues of other products but lower costs to obtain the gross profits, and where depreciation is used as tax shields, then taxes are deducted, etc.), and both positive and negative correlations may exist between the various revenues (e.g., similar product lines versus competing product lines cannibalizing each other’s revenues), the only way to determine the final effect is through simulations.
- Correlations typically affect only the second moment (risk) of the distribution, leaving the first moment (mean or expected returns) relatively stable. There is an unknown effect on the third and fourth moments (skew and kurtosis), and only after a simulation is run can the outcomes be empirically determined because the effects are wholly dependent on the distributions’ type, skew, kurtosis, and shape. Therefore, in traditional single-point estimates where only the first moment is determined, correlations will not affect the results. When simulation models are used, the entire probability distribution of the results is obtained and, hence, correlations are critical.
- Correlations should be used in a simulation if there are historical data to compute its value. Even in situations without historical data but with clear theoretical justifications for correlations, one should still input them. Otherwise, the distributional spreads would not be accurate. For instance, a demand curve is theoretically negatively sloped (negatively correlated), where the higher the price, the lower the quantity demanded (due to income and substitution effects) and vice versa. Therefore, if no correlations are entered in the model, the simulation results may randomly generate high prices with high quantity demanded, creating extremely high revenues, as well as low prices and low quantity demanded, creating extremely low revenues. The simulated probability distribution of revenues would, hence, have wider spreads into the left and right tails. These wider spreads are not representative of the true nature of the distribution. Nonetheless, the mean or expected value of the distribution remains relatively stable. It is only the percentiles and confidence intervals that get biased in the model.
- Therefore, even without historical data, if we know that correlations do exist through experimentation, widely accepted theory, or even simply by logic and guesstimates, one should still input approximate correlations into the simulation model. This approach is acceptable because the first moment or expected values of the final results will remain unaffected (only the risks will be affected as discussed). Typically, the following approximate correlations can be applied even without historical data:
- Use 0.00 if there are no correlations between variables.
- Use ±0.25 for weak correlations (use the appropriate sign).
- Use ±0.50 for medium correlations (use the appropriate sign).
- Use ±0.75 for strong correlations (use the appropriate sign).
- It is theoretically very difficult, if not impossible, to have large sets of empirical data from real-life variables that are perfectly uncorrelated (i.e., a correlation of 0.0000000… and so forth). Therefore, given any random data, adding additional variables will typically increase the total absolute values of correlation coefficients in a portfolio (R-squared always increases, which is why in the forecasting chapters we introduce the concept of Adjusted R-squared, which accounts for the marginal increase in total correlation compared against the number of variables; for now, think of Adjusted R-squared as the adjustment to R-squared by taking into account garbage correlations). Therefore, it is usually important to perform statistical tests on correlation coefficients to see if they are statistically significant or their values can be considered random and insignificant. For example, we know that a correlation of 0.9 is probably significant, but what about 0.8, or 0.7, or 0.3, and so forth? That is, at what point can we statistically state that a correlation is insignificantly different from zero; would 0.10 qualify, or 0.05, or 0.03, and so forth?
- The t-test with n – 2 degrees of freedom hypothesis test can be computed by taking
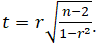 The null hypothesis is such that the population correlation p = 0.
The null hypothesis is such that the population correlation p = 0. - There are other measures of dependence such as Kendall’s τ, Brownian correlation, Randomized Dependence Coefficient (RDC), entropy correlation, polychoric correlation, canonical correlation, and copula-based dependence measures. These are less applicable to most empirical data and are not as popular or applicable in most situations.
- Finally, here are some notes in applying and analyzing correlations in Risk Simulator:
- Risk Simulator uses the Normal, T, and Quasi-Normal Copula methods to simulate correlated variable assumptions. The default is the Normal Copula, and it can be changed within the Risk Simulator | Options menu item. The T Copula is similar to the Normal Copula but allows for extreme values in the tails (higher kurtosis events), and the Quasi-Normal Copula simulates correlated values between the Normal and T Copulas.
- After setting up at least two or more assumptions, you can set correlations between pairwise variables by selecting an existing assumption and using the Risk Simulator | Set Input Assumption dialog.
- Alternatively, the Risk Simulator | Analytical Tools | Edit Correlations menu item can be used to enter multiple correlations using a correlation matrix.
- If historical data from multiple variables exist, by performing a distributional fitting using Risk Simulator | Analytical Tools | Distributional Fitting (Multi-Variable), the report will automatically generate the best-fitting distributions with their pairwise correlations computed and entered as simulation assumptions. In addition, this tool allows you to identify and isolate correlations that are deemed statistically insignificant using a two-sample t-test.

