File Names: Real Options – Simple Two-Phased Simultaneous Compound Option; Real Options – Multiple-Phased Simultaneous Compound Option
Location: Modeling Toolkit | Real Options Models
Brief Description: Computes simultaneous compound options with multiple options executed simultaneously with complex interrelationships between phases and customizable and changing input parameters
Requirements: Modeling Toolkit, Real Options SLS
The Simultaneous Compound Option evaluates a project’s strategic value when the value of the project depends on the success of two or more investment initiatives executed simultaneously in time. The Sequential Compound Option evaluates these investments in stages, one after another over time, while the simultaneous option evaluates these options concurrently. Clearly, the sequential compound is worth more than the simultaneous compound option by virtue of staging the investments. Note that the simultaneous compound option acts like a regular execution call option. Hence, the American Call Option is a good benchmark for such an option.
Real Options – Two-Phased Simultaneous Compound Option
Figure 192.1 shows how a Simultaneous Compound Option can be solved using the SLS (example file used: Simple Two-Phased Simultaneous Compound Option). Like the sequential compound option analysis, the existence of an option value implies that the ability to defer and wait for additional information prior to executing is valuable due to the significant uncertainties and risks as measured by Volatility. However, when the cost of waiting as measured by the Dividend Rate is high, the option to wait and defer becomes less valuable, until the break-even point where the option value equals zero and the strategic project value equals the NPV of the project. This break-even point gives the decision maker valuable insights into the interactions between the levels of uncertainty inherent in the project and the cost of waiting to execute.
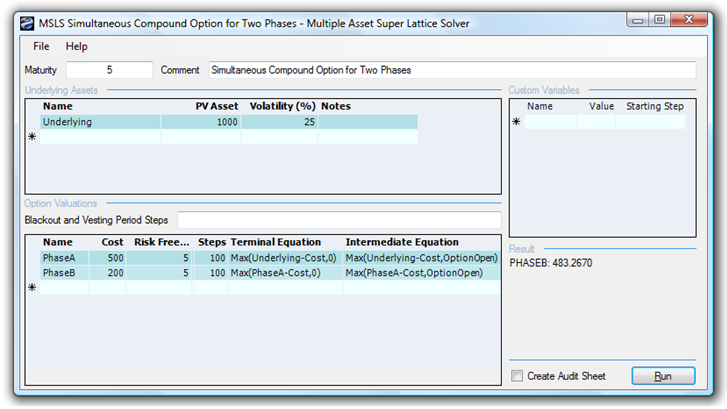
Figure 192.1: Solving a simultaneous compound option using SLS
Real Options – Multiple-Phased Simultaneous Compound Option
The same analysis can be extended to Multiple Investment Simultaneous Compound Options as seen in Figure 192.2 (example file used: Multiple-Phased Simultaneous Compound Option).
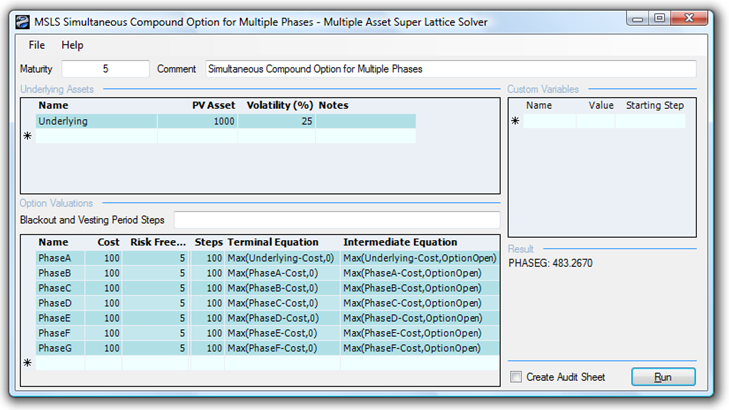
Figure 192.2: Solving a multiple investment simultaneous compound option using SLS
Exercise: Simultaneous Compound Option
In a compound option analysis, the value of the option depends on the value of another option. For instance, a pharmaceutical company currently going through a particular Food and Drug Administration (FDA) drug approval process has to go through human trials. The success of the FDA approval depends heavily on the success of human testing, both occurring at the same time. Suppose that the former costs $900 million and the latter $500 million. Further, suppose that both phases occur simultaneously and take five years to complete. Using Monte Carlo simulation, you calculate the implied volatility of the logarithmic returns on the projected future cash flows to be 25%. The risk-free rate on a riskless asset for the next five years is found to be yielding 7.7%. The drug development effort’s static valuation of future profitability using a DCF model (in other words, the present value of the future cash flows discounted at an appropriate market risk-adjusted discount rate) is found to be $1 billion. Do the following exercises, answering the questions posed:
- Solve the simultaneous compound option problem manually using a 10-step lattice and confirm the results by generating an Audit Sheet using the software.
- Swap the implementation costs such that the first cost is $500 and the second cost is $900. Is the resulting option value similar or different? Why?
- What happens when part of the cost of the first option is allocated to the second option? For example, make the first cost $450 and the second cost $950. Does the result change? Explain.
- Show how a Closed-Form American Approximation Model can be used to benchmark the results from a simultaneous compound option.
- Show how a Sequential Compound Option can also be used to calculate or at least approximate the simultaneous compound option result.
- Assume that the total $1,400 implementation cost (in present values) is now distributed equally across seven simultaneous Does the result change? Why or why not?

