File Name: Real Options – Mean-Reverting Calls and Puts Using Trinomial Lattices
Location: Modeling Toolkit | Real Options Models
Brief Description: Computes the options where the underlying asset follows a mean-reverting process (e.g., interest rates), using trinomial lattices
Requirements: Modeling Toolkit, Real Options SLS
The Mean-Reversion Option in the SLS software calculates both the American and European options when the underlying asset value is mean reverting. A mean-reverting stochastic process reverts back to the long-term mean value (Long-Term Rate Level) at a particular speed of reversion (Reversion Rate). Examples of variables following a mean-reversion process include inflation rates, interest rates, gross domestic product growth rates, optimal production rates, price of natural gas, and so forth. Certain variables such as these succumb either to natural tendencies or economic/business conditions to revert to a long-term level when the actual values stray too far above or below this level. For instance, monetary and fiscal policy will prevent the economy from significant fluctuations, while policy goals tend to have a specific long-term target rate or level. Figure 188.1 illustrates a regular stochastic process (dotted line) versus a mean-reversion process (solid line). Clearly, the mean-reverting process with its dampening effects will have a lower level of uncertainty than the regular process with the same volatility measure.
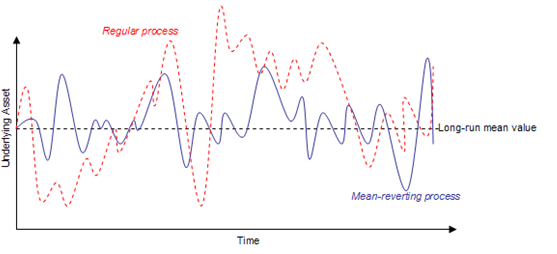 Figure 188.1: Mean reversion in action
Figure 188.1: Mean reversion in action
Figure 188.2 shows the mean-reverting call option computed using the SLS Multinomial Lattice module. Using this module, we can compute additional call and put results from a regular option modeled using the Trinomial Lattice versus calls and puts assuming a mean-reverting (MR) tendency of the underlying asset using the Mean-Reverting Trinomial Lattice. Based on the results, several items are worthy of notice:
- The MR Calls ≤ regular Calls because of the dampening effect of the mean-reversion asset. The MR asset value will not increase as high as the regular asset value.
- Conversely, the MR Puts ≥ regular Puts because the asset value will not rise as high, indicating that there will be a higher chance that the asset value will hover around the PV Asset, and a higher probability it will be below the PV Asset, making the put option more valuable.
- With the dampening effect, the MR Call and MR Put ($18.62 and $18.76) are more symmetrical in value than with a regular call and put ($31.99 and $13.14).
- The regular American Calls = regular European Calls without dividends because, without dividends, it is never optimal to execute early. However, because of the mean-reverting tendencies, being able to execute early is valuable, especially before the asset value So, we see that MR American Calls > MR European Calls but, of course, both are less than the regular Calls.
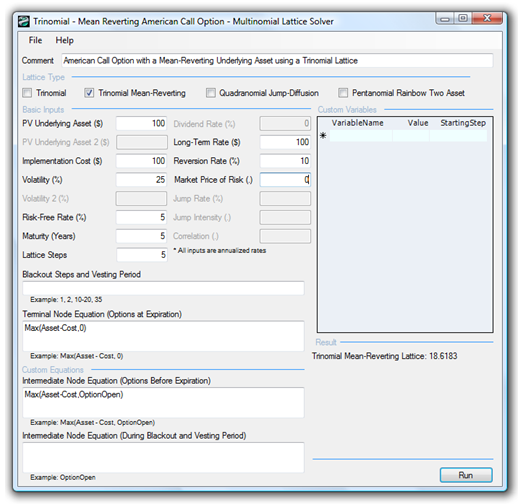
Figure 188.2: Comparing mean-reverting calls and puts to regular calls and puts
Other items of interest in mean-reverting options include:
- The higher (lower) the long-term rate level, the higher (lower) the call options.
- The higher (lower) the long-term rate level, the lower (higher) the put options.
Finally, be careful when modeling mean-reverting options. Higher lattice steps usually are required, and certain combinations of reversion rates, long-term rate level, and lattice steps may yield unsolvable trinomial lattices. When this occurs, the software will return error messages.

