File Names: Real Options – Expand Contract Abandon American and European Option; Real Options – Expand Contract Abandon Bermudan Option; Real Options – Expand Contract Abandon Customized Option I; Real Options – Expand Contract Abandon Customized Option II
Location: Modeling Toolkit | Real Options Models
Brief Description: Models a combination of mutually exclusive chooser options (contraction, expansion, and abandonment) with customizable inputs
Requirements: Modeling Toolkit, Real Options SLS
The Contraction, Expansion, and Abandonment Option applies when a firm has three competing and mutually exclusive options on a single project to choose from at different times up to the time of expiration. Be aware that this is a mutually exclusive set of options. That is, you cannot execute any combinations of expansion, contraction, or abandonment at the same time. Only one option can be executed at any time.
For mutually exclusive options, use a single model to compute the option value as seen in Figure 183.1 (Expand Contract Abandon American and European Option). However, if the options are not mutually exclusive, calculate them individually in different models and add up the values for the total value of the strategy.
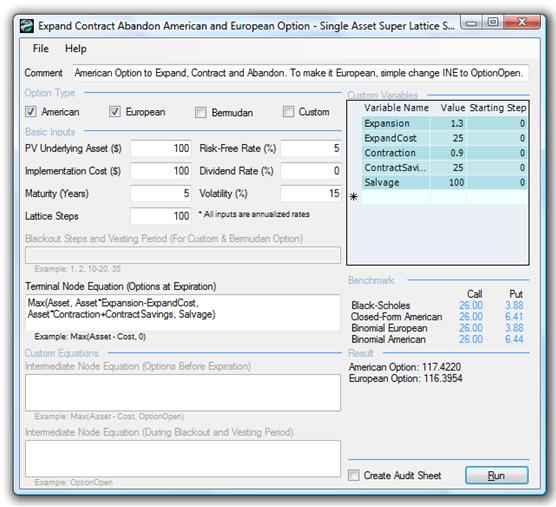
Figure 183.1: American, European, and custom options to expand, contract, and abandon
Figure 183.2 illustrates a Bermudan Option with the same parameters but with certain blackout periods (example file used: Expand Contract Abandon Bermudan Option), while Figure 183.3 (example file used: Expand Contract Abandon Customized Option I) illustrates a more complex Custom Option where during some earlier period of vesting, the option to expand does not exist yet (perhaps the technology being developed is not yet mature enough in the early stages to be expanded into some spin-off technology). In addition, during the post-vesting period but prior to maturity, the option to contract or abandon does not exist. Perhaps the technology is now being reviewed for spin-off opportunities, and so forth. Figure 183.4 uses the same example as in Figure 183.3, but now the input parameters (salvage value) are allowed to change over time, perhaps accounting for the increase in project, asset, or firm value if abandoned at different times (example file used: Expand Contract Abandon Customized Option II).
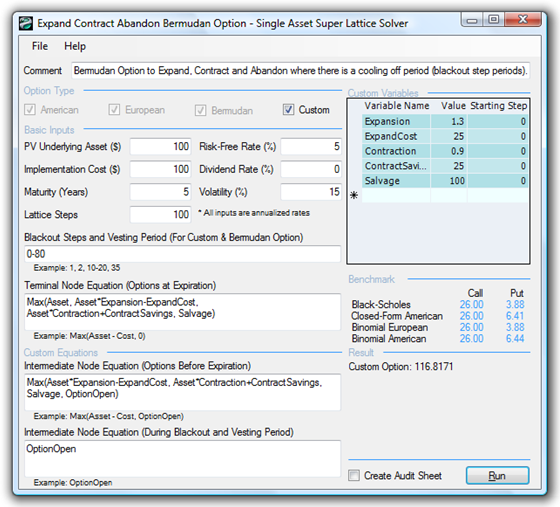
Figure 183.2: Bermudan option to expand, contract, and abandon
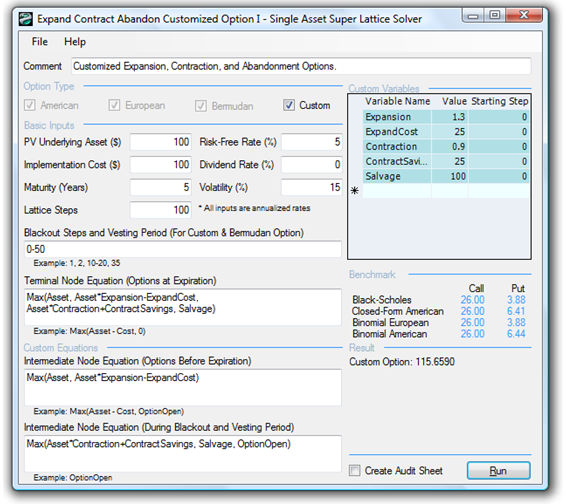
Figure 183.3: Custom options with mixed expand, contract, and abandon capabilities
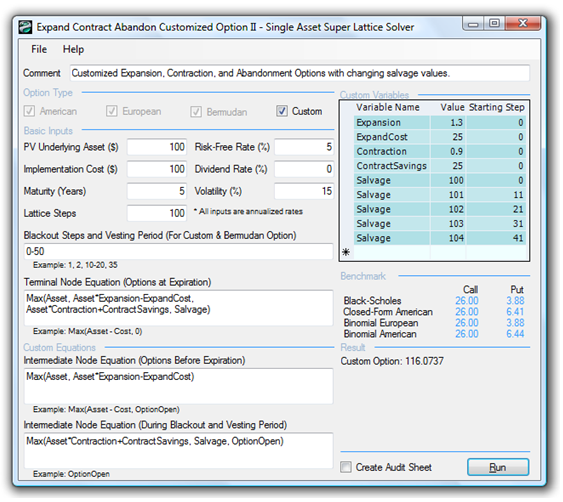
Figure 183.4: Custom options with mixed expand, contract, and abandon capabilities with changing input parameters
Exercise: Option to Choose – Contraction, Expansion, Abandonment (Dominant Option)
Suppose a large manufacturing firm decides to hedge itself through the use of strategic options. Specifically, it has the option to choose among three strategies: expanding its current manufacturing operations, contracting its manufacturing operations, or completely abandoning its business unit at any time within the next five years. Suppose the firm has a current operating structure whose static valuation of future profitability using a DCF model (in other words, the present value of the future cash flows discounted at an appropriate market risk-adjusted discount rate) is found to be $100 million.
Using Monte Carlo simulation, you calculate the implied volatility of the logarithmic returns on the projected future cash flows to be 15%. The risk-free rate on a riskless asset for the next five years is found to be yielding 5% annualized returns. Suppose the firm has the option to contract 10% of its current operations at any time over the next five years, thereby creating an additional $25 million in savings after this contraction. The expansion option will increase the firm’s operations by 30%, with a $20 million implementation cost. Finally, by abandoning its operations, the firm can sell its intellectual property for $100 million. Do the following exercises, answering the questions posed:
following exercises, answering the questions posed:
- Solve the chooser option problem manually using a 10-step lattice and confirm the results by generating an audit sheet using the SLS software.
- Recalculate the option value in exercise 1 accounting only for an expansion option.
- Recalculate the option value in exercise 1 accounting only for a contraction option.
- Recalculate the option value in exercise 1 accounting only for an abandonment option.
- Compare the results of the sum of these three individual options in exercises 2 to 4 with the results obtained in exercise 1 using the chooser option.
-
- Why are the results different?
- Which value is correct?
- Prove that if there are many interacting options, if there is a single dominant strategy, then the value of the project’s option value approaches this dominant strategy’s value. That is, perform the following steps, then compare and explain the results.
- Reduce the expansion cost to $1.
- Increase the contraction savings to $100.
- Increase the salvage value to $150.
- What inferences can you make based on these results?
- Solve this Contraction and Abandonment option: Asset value of $100, five-year economic life, 5% annualized risk-free rate of return, 25% annualized volatility, 25% contraction with a $25 savings, and a $70 abandonment salvage value.
- Show and explain what happens when the salvage value of abandonment far exceeds any chances of a contraction. For example, set the salvage value at $200.
- In contrast, set the salvage value back to $70, and increase the contraction savings to $100. What happens to the value of the project?
- Solve just the contraction option in isolation. That is, set the contraction savings to $25 and explain what happens. Change the savings to $100 and explain the change in results. What can you infer from dominant option strategies? Solve just the abandonment option in isolation. That is, set the salvage value to $70, and explain what happens. Change the salvage value to $200, and explain the change in results. What can you infer from dominant option strategies?

