File Name: Analytics – Weighting of Ratios
Location: Modeling Toolkit | Analytics | Weighting of Ratios
Brief Description: Illustrates how weighted averages are computed and how sometimes picking the wrong weighting factor results in wrong answers
Requirements: Modeling Toolkit
This is a simple example model illustrating how choosing the weighting factor is critical in obtaining the correct answer to a weighted average approach. In Example 1, we see a portfolio of 8 projects, each with its own revenue, cost, and return on investment (ROI) values (Figure 9.1). The idea is to compute the total portfolio ROI given these various projects. This first example illustrates that given a simple identical allocation of cost, revenues, and ROI, you can just compute the average of the total ROI, and this yields the correct ROI for the portfolio. However, in Example 2, we have a set of very different projects, which is oftentimes the case in real life, with different costs, revenues, and individual ROIs.
Using a simple sum or simple average will yield grossly misleading results. For instance, a grossly inflated sum yields a value of 3,900% ROI, while the average per project yields a value of 487.59%, which are both incorrect. The correct ROI for the total portfolio should be 288.08% (as confirmed by summing the total costs and total revenues for all projects in the portfolio and then computing the ROI for this portfolio level), as seen in Figure 9.1.
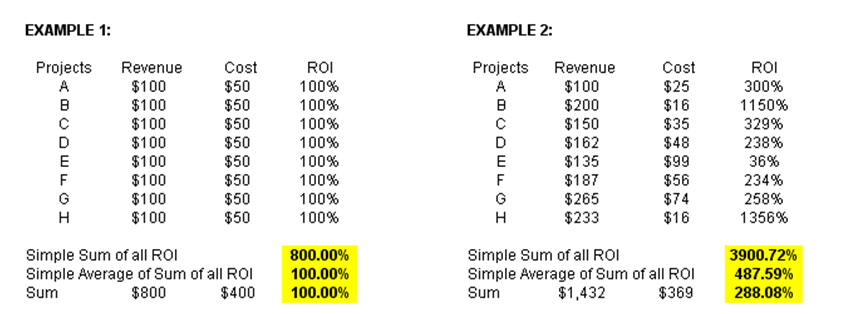
Figure 9.1: Weighting of ratios
The same result can be obtained through a weighted average of the ROI. However, choosing the right weighting factor is critical. For instance, in the examples provided, we wanted to determine the total portfolio ROI, which is computed as (Returns – Cost)/Cost, which means that the denominator, in this case, is Cost. If we choose cost as the weighting factor, we get the correct answer of 288.08%. Had we chosen revenues as the weighting factor, we get an incorrect answer (Figure 9.2). Therefore, weighted averages and weighting factors are important when determining portfolio totals. This is a simple concept but its importance and potentials for error are often overlooked.
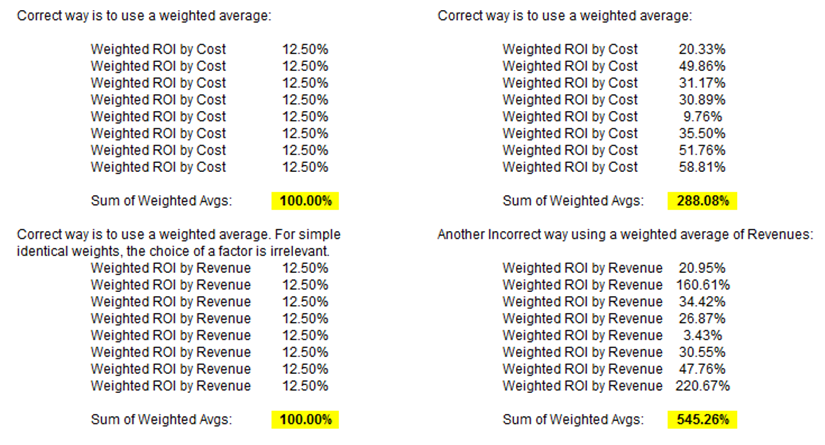
Figure 9.2: Different weighting schemes

