File Name: Risk Analysis – Interest Rate Risk
Location: Modeling Toolkit | Risk Analysis | Interest Rate Risk
Brief Description: Applies duration and convexity measures to account for a bond’s sensitivity and how interest rate shifts can affect the new bond price, and how this new bond price can be approximated using these sensitivity measures
Requirements: Modeling Toolkit, Risk Simulator
Modeling Toolkit Functions Used: MTBondPriceDiscrete, MTModifiedDuration, MTConvexityDiscrete
Banks selling fixed-income products and vehicles need to understand interest-rate risks. This model uses duration and convexity to show how fixed-income products react under various market conditions. To compare the effects of interest rate and credit risks on fixed-income investments, this model uses modified duration and convexity (discrete discounting) to analyze the effects of a change in interest rates on the value of a bond or debt (Figure 2.21).
Duration and convexity are sensitivity measures that describe exposure to parallel shifts in the spot interest rate yield curve, applicable to individual fixed income instruments or entire fixed income portfolios. These sensitivities cannot warn of exposure to more complex movements in the spot curve, including tilts and bends, only parallel shifts. The idea behind duration is simple. Suppose a portfolio has a duration measure of 2.5 years. This means that the portfolio’s value will decline about 2.5% for each 1% increase in interest rates—or rise about 2.5% for each 1% decrease in interest rates. Typically, a bond’s duration will be positive but exotic instruments such as mortgage-backed securities may have negative durations, or portfolios that short fixed income instruments or pay fixed for floating on an interest rate swap. Inverse floaters tend to have large positive durations. Their values change significantly for small changes in rates. Highly leveraged fixed income portfolios tend to have very large (positive or negative) durations.
In contrast, convexity summarizes the second-most significant piece of information, or the nonlinear curvature of the yield curve, whereas duration measures the linear or first-approximation sensitivity. Duration and convexity have traditionally been used as tools for immunization or asset-liability management. To avoid exposure to parallel spot curve shifts, an organization (such as an insurance company or defined benefit pension plan) with significant fixed income exposures might perform duration matching by structuring its assets so that their duration matches the duration of its liabilities so the two offset each other. Even more effective (but less frequently practical) is duration-convexity matching, in which assets are structured so that durations and convexities match.
![]()
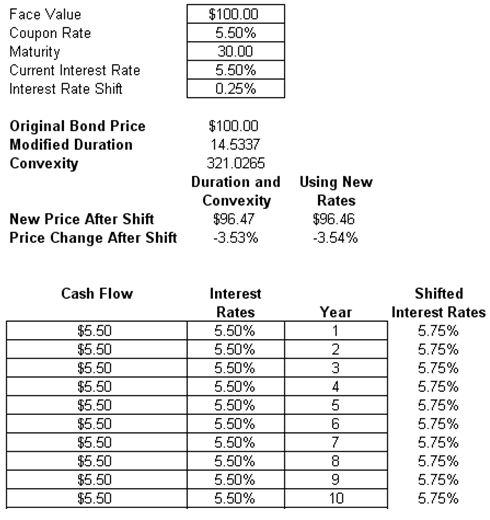
Figure 2.21: Interest Rate Risk

