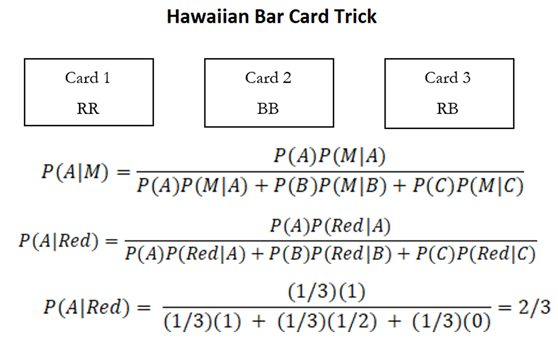
Other simple example applications are the Hawaiian bar card trick that I just made up or the old Monty Hall television game show. In the bar trick, suppose you take a nice trip to Maui and hang out at a local bar. Three hours later, you are bored and start thinking about a game to play with the attractive hostess. You take out three blank cards and write something down on each of the six sides. On the first card, you have Red and Red, the second card has Black and Black, and the third card has Red and Black. You then cover the cards with a napkin, and shuffle them, and proceed to ask the hostess to take one card out, showing only the top. Neither of you sees the bottom of the card. Now, suppose the top of the card says Red. You then insist that being the gentleman you are, you will also follow the young lady’s lead and select Red on the bottom. If the bottom is indeed Red, you win, but if it is Black, the hostess wins. You then proceed to tell a fake statistical tale. You say that since the top card is Red, there is no way it is the Black-Black card. Therefore, it must be either the Red-Red or Red-Black card, thereby having a 50:50 chance of being either Red or Black. And the payoff is that if you win, she brings you a free drink, but if she wins, you will double her tip (by the way, you have not yet told her what her tip was going to be, so, the double of nothing is still nothing, or the double of something fairly little is still little). The question is, what is the probability that you win or that she wins? In this situation, a Bayes-update calculation is needed, and we can boldly say that the chances of being Red or Black are not 50%.
The calculations are shown next, however, before we jump into the math, it would be nice to understand the concept a little better and see if we can answer the question as to who wins (i.e., is the bottom of the card Red or Black) using basic logic. As mentioned, it can never be the Black-Black card. Hence, we are left with only the Red-Black or Red-Red card. Now, if you had selected the Red-Black card with the Red showing, then the other side must be Black. Score one for the Black team. Next, if she had selected the Red-Red card, you both could have been looking at the first side of the Red-Red card, or the second side of the Red-Red card. And in either scenario, the other side is Red, meaning there are two possible Red outcomes. Hence, the probability of Red at the bottom is 2/3 and the probability of Black at the bottom is 1/3.