File Names: Six Sigma – Statistical Capability; Six Sigma – Unit Capability; Six Sigma – Control Charts
Location: Modeling Toolkit | Six Sigma
Brief Description: Illustrate how to obtain the various capability measures such as the capability index (Cpk and Cp), yields, defects per million opportunities (DPMO), and others
Requirements: Modeling Toolkit, Risk Simulator
Modeling Toolkit Functions Used: MTSixSigmaStatCP, MTSixSigmaStatCPK, MTSixSigmaStatDPU, MTSixSigmaStatDPMO, MTSixSigmaStatProcessSigma, MTSixSigmaUnitDPU, MTSixSigmaUnitDPMO, MTSixSigmaUnitYield, MTSixSigmaUnitCPK, MTSixSigmaUnitProcessSigma
Capability Measures (Cp and Cpk) and Specification Levels (USL and LSL)
Capability measures in Six Sigma are the central analytics in quality control. Defective Proportion Units (DPUs) are the number of defects observed with respect to the total opportunities or outcomes, and can be measured with respect to a million opportunities (defective parts per million, DPPM, or also known as the defects per million opportunities, DPMO). The Process Capability Index or Cpk takes into account the off-centered distribution and analyzes it as a centered process producing a similar level of defects (defined as the ratio between permissible deviation, measured from the mean value to the nearest specific limit of acceptability, and the actual one-sided 3-sigma spread of the process). Simplistically, it measures how many times you can fit three standard deviations of the process between the mean of the process and the nearest specification limit. Assuming that the process is stable and predictable, if you can do this once, Cpk is 1, and your process probably needs attention. If you can do it 1.5 times, your process is excellent, and you are on the path to being able to discontinue the final inspection. If you can do it twice, you have an outstanding process. If Cpk is negative, the process mean is outside the specification limits. Cpk of at least 1.33 is desired. Finally, the sigma of the process is determined. Typically, this process sigma value can be used to compare before and after effects of some quality improvement program, or to see if the process is up to par in terms of a target sigma level.
This statistical capability model uses as inputs the statistical properties of the process, including the observed mean and standard deviation (sigma), as well as predefined lower and upper specification limits (LSLs and USLs). In contrast, the Unit Capability model computes some of the same capability measures but uses the actual number of defects and population size. In addition, the Cp index is computed, which relates to the potential of the process to meet specification, regardless of where the process distribution falls. The process may not be performing within specifications, but the index tells you how the process will perform if you can shift the distribution mean to the desired target (without changing the distribution). If we have a Cp of 2.0, it has the potential to be a Six Sigma process. In contrast, Cpk actually compares the distribution of the data to the specification limits to determine its actual performance. If we have a Cpk of 2.0, you have a Six Sigma process. As discussed, a Cpk of at least 1.33 is desired, and 1.5 is excellent. See Figure 149.1.
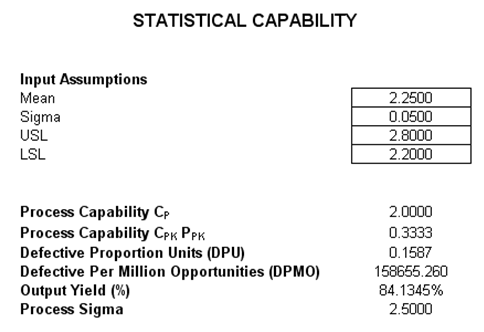Figure 149.1: Six Sigma capability modeling
Quality Control Charts
Sometimes the specification limits are not set; instead, statistical control limits are computed based on the actual data collected (e.g., the number of defects in a manufacturing line). For instance, in Figure 149.2, we see 20 sample experiments or samples taken at various times of a manufacturing process. The number of samples taken varied over time, and the number of defective parts was also gathered. The upper control limit (UCL) and lower control limit (LCL) are computed, as are the central line (CL) and other sigma levels. The resulting chart is called a control chart, and if the process is out of control, the actual defect line will be outside of the UCL and LCL lines. Typically, when the LCL is a negative value, we set the floor as zero, as illustrated in Figure 149.2.
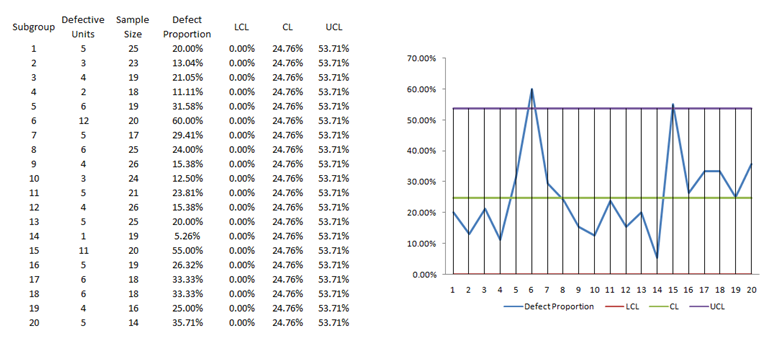
Figure 149.2: Example quality control p-chart
In the interpretation of a control chart, by adding in the +/– 1 and 2 sigma lines, we can divide the control charts into several areas or zones, as illustrated in Figure 149.3. The following are rules of thumb that typically apply to control charts to determine if the process is out of control:
- If one point is beyond Area A
- If two out of three consecutive points are in Area A or beyond
- If four out of five consecutive points are in Area B or beyond
- If eight consecutive points are in Area C or beyond
Additionally, a potential structural shift can be detected if any one of the following occurs:
- At least 10 out of 11 sequential points are on one side of the CL
- At least 12 out of 14 sequential points are on one side of the CL
- At least 14 out of 17 sequential points are on one side of the CL
- At least 16 out of 20 sequential points are on one side of the CL
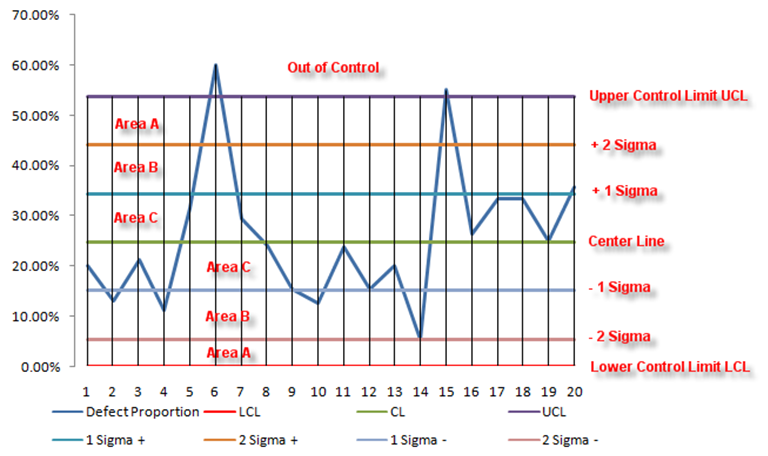
Figure 149.3: Interpreting control charts
The Modeling Toolkit presents several control chart types, and each type is used under different circumstances:
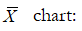used when the variable has raw data values and there are multiple measurements in a sample experiment, and multiple experiments are run, and the average of the collected data is of interest.
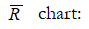used when the variable has raw data values and there are multiple measurements in a sample experiment, and multiple experiments are run, and the range of the collected data is of interest.- XmR chart: used when the variable has raw data values and is a single measurement taken in each sample experiment, and multiple experiments are run, and the actual value of the collected data is of interest.
- P-chart: used when the variable of interest is an attribute (e.g., defective or non-defective) and the data collected are in proportions of defects (or the number of defects in a specific sample) and there are multiple measurements in a sample experiment, and multiple experiments are run, and the average proportion of defects of the collected data is of interest, also, the number of samples collected in each experiment differs.
- NP-chart: used when the variable of interest is an attribute (e.g., defective or non-defective) and the data collected are in proportions of defects (or the number of defects in a specific sample) and there are multiple measurements in a sample experiment, and multiple experiments are run, and the average proportion of defects of the collected data is of interest, also, the number of samples collected in each experiment is constant for all experiments.
- C-chart: used when the variable of interest is an attribute (e.g., defective or non-defective) and the data collected are in the total number of defects (actual count in units) and there are multiple measurements in a sample experiment, and multiple experiments are run, and the average number of defects of the collected data is of interest, also, the number of samples collected in each experiment the same.
- U-chart: used when the variable of interest is an attribute (e.g., defective or non-defective) and the data collected are in the total number of defects (actual count in units) and there are multiple measurements in a sample experiment, and multiple experiments are run, and the average number of defects of the collected data is of interest, also, the number of samples collected in each experiment differs.
The majority of students aren’t aware that they require assistance with their writing essay until their deadline is near. Procrastination is a strange mental process that convinces our brains that everything is fine as https://www.baltictimes.com/the_best_college_paper_writing_services/ we slack off on a crucial project. This may cause anxiety after the deadline is set. If students aren’t able to meet the deadlines, students who are responsible might be able to seek help writing papers. These tips will assist you to decide if you should use writing assistance from a professional.
