File Name: Options Analysis – Options Adjusted Spreads on Debt
Location: Modeling Toolkit | Options Analysis | Options Adjusted Spreads on Debt
Brief Description: Computes the option-adjusted spread, that is, the additional premium that should be charged on the option provision
Requirements: Modeling Toolkit
Modeling Toolkit Functions Used: MTBDTInterestRateLattice, MTBDTNoncallableDebtPriceLattice, MTBDTCallableDebtPriceLattice
Certain types of debt come with an option-embedded provision; for instance, a bond might be callable if the market price exceeds a certain value (when prevailing interest rates drop, making it more profitable for the issuing company to call the debt and reissue new ones at the lower rate) or have a prepayment allowance of mortgages or lines of credit and debt. Options-adjusted spreads, or OAS, value the spread between a straight bond and a bond with some embedded options, such as callability covenants, and are used to create modified binomial lattices to value such instruments, assuming changing interest rates and volatilities over time.
Figure 108.1 illustrates the OAS Lattice model with a set of sample inputs. The interest rates are assumed to be changing over time, with changing instantaneous volatilities, as in real life, where the yield curve or term structure of interest rates changes over time and has different volatilities at different ends of the curve. The entire yield curve may shift, twist, or bend, with higher maturity. See the Yield Curve – Term Structure of Volatility chapter for details on how to compute interest rate volatilities and the typical characteristics of volatility smiles and frowns.
Setting up this model is very similar to the one shown in Chapter 106 on the inverse floater bonds. Please review that chapter on how to create the lattice matrix as well as for information on calibrating the underlying interest rate lattice to make sure it models the term structure of interest rates and the corresponding localized volatilities of interest rates.
Note that one of the key inputs in the model is the call price of the bond and the time to call, translated into time steps. For instance, in a four-year debt modeled using an eight-step lattice, if the bond is callable starting in the third year, then the callable step is set as 6. Note that this model is the same as the last two chapters; the main difference being that this model allows you to generate your own modified binomial lattices to any number of steps. Be careful as the higher the number of steps, the longer it takes to generate and compute the lattices, depending on your computer’s processor speed.
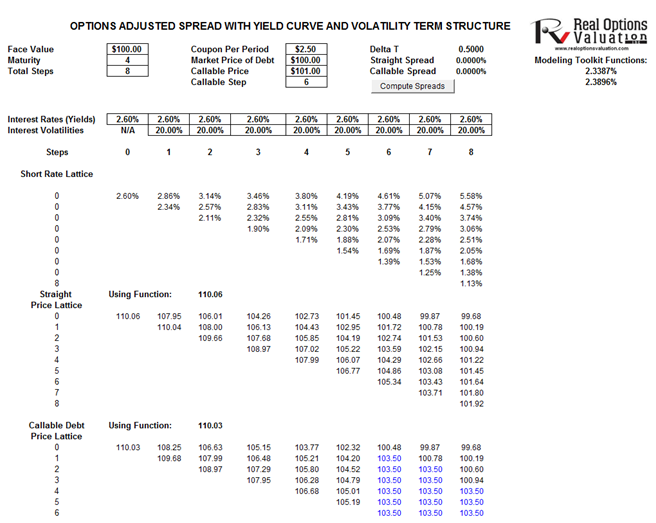
Figure 108.1: Options-adjusted spreads lattice

