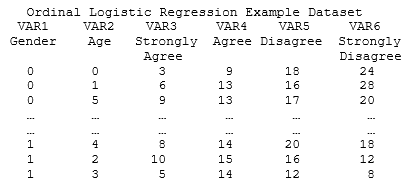
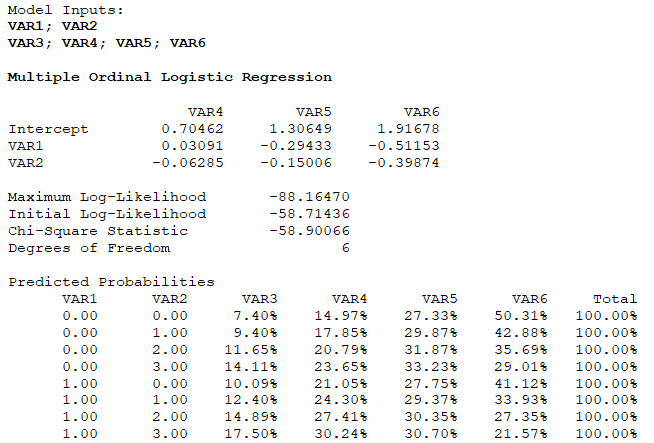
An Ordinal Logistic regression runs a multivariate ordinal logistic regression with two predictor variables and multiple frequencies of ordered variables, for instance, the two categorical variables of Gender (0/1) and Age (1–5), with five variables filled with the numbers or frequencies of people who responded Strongly Agree, Agree, Neutral, Disagree, or Strongly Disagree, which are presumably ordered. Note that this is an ordinal dataset where the Age variables are ordered, and it is multinomial because we are forecasting the four variables VAR3–VAR6 values.
Note that this is an extension of the binary logistic model, but in this example, there are multiple probabilities or frequency forecasts (VAR3–VAR6). Alternatively, you can collapse these four variables into a single variable and run the Logit regression multiple times. For instance, combine these four variables into a single variable that is binary (e.g., Strongly Agree = 1 and All Others = 0) to run a Logit model. Then, repeat the process with Agree = 1 and All Others = 0, and repeat the process. Remember to run only k-1 models, where k is the number of frequency or count variables, and the last variable’s predicted probability should be the complement of the remaining variables such that the total probability equals 100%. Hence, in the results below, although there are four variables VAR3–VAR6, the results only return VAR4–VAR6.
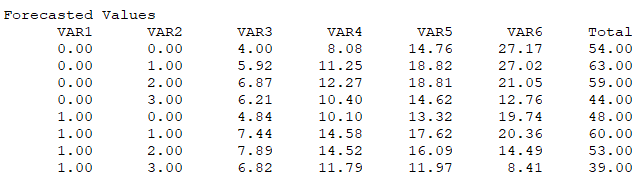
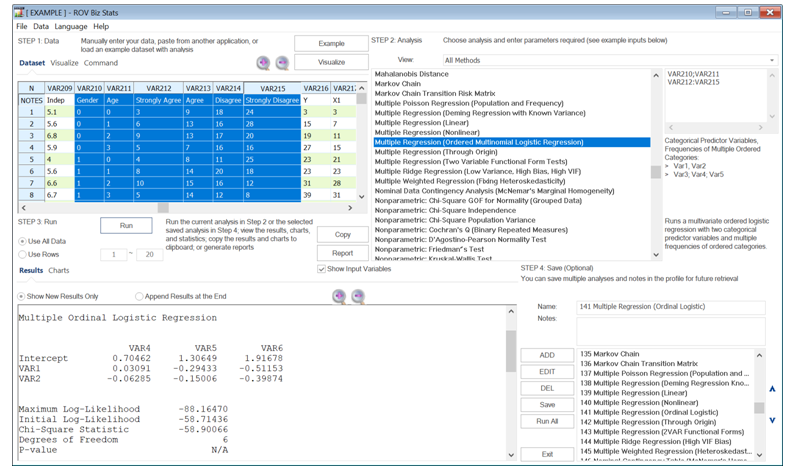
The following illustrates some sample datasets used in BizStats, the required input parameter format, and the results. Typically, the computed coefficients are interpreted in a log-logistic function and can seem complicated at times. Nonetheless, it is much simpler to look at the predicted probabilities (relative frequencies) and forecasted values (frequencies) given all the possible combinations of the two predictor variables of gender and age. Unfortunately, this approach can only accommodate two predictor variables. If more predictors are needed, use the Logit model as described above.