The binomial distribution describes the number of times a particular event occurs in a fixed number of trials, such as the number of heads in 10 flips of a coin or the number of defective items out of 50 items chosen.
The three conditions underlying the binomial distribution are:
- For each trial, only two outcomes are possible that are mutually exclusive.
- Trials are independent––what happens in the first trial does not affect the next trial.
- The probability of an event occurring remains the same from trial to trial.
The mathematical constructs for the binomial distribution are as follows:
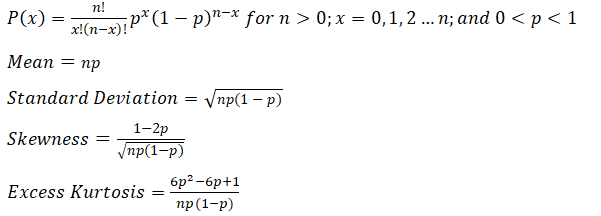
The probability of success (p) and the integer number of total trials (n) are the distributional parameters. The number of successful trials is denoted x. It is important to note that probability of success (p) of 0 or 1 are trivial conditions and do not require any simulations, and, hence, are not allowed in the software.
Input requirements:
0 < Probability of success < 1 (that is, 0.0001 ≤ p ≤ 0.9999)
Number of trials ≥ 1 or positive integers and ≤ 1000 (for larger trials, use the normal distribution with the relevant computed binomial mean and standard deviation as the normal distribution’s parameters).
Note that the binomial distribution requires the following:
- Two outcomes in each trial — success or failure.
- Constant probability of success (p) or failure (1 – p).
- Statistical independence between trials.
- The probability (p) must be constant over time.
For example, if n = 100 toilet rolls, try calculating the P(x = 1) when p = 0.5 and P(x = 2). Or consider that when n = 10, we are assuming a sampling without replacement, hence, the probability changes and is no longer constant. So, in a binomial distribution, we are assuming a large enough population that sampling without replacement is almost the same as sampling with replacement. In such situations, using the hypergeometric distribution is preferable.
Examples: Discrete Distribution – Binomial
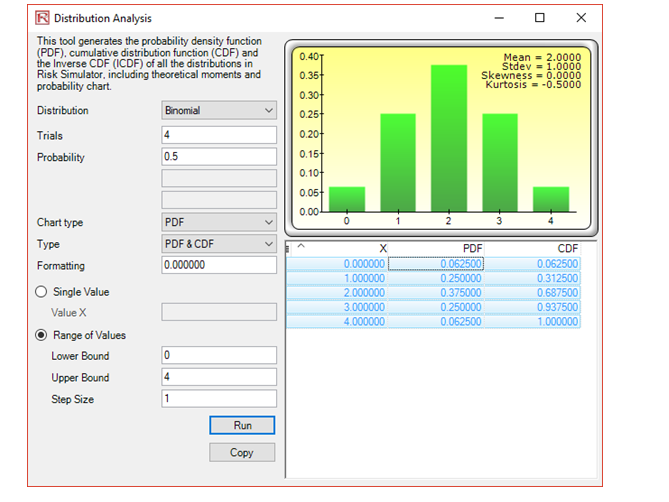
Example 1: If 50% of all tissue rolls are short and you select 4 rolls at random, complete the following probabilities:
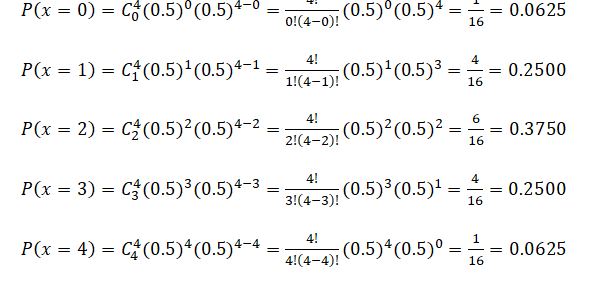
If you draw this probability distribution, what does it look like?
Example 2: Before modern medicine was able to detect the sex of a fetus (chorionic villus sampling, for the science freaks out there), psychics have long claimed to be able to predict the sex of the unborn child by looking at a picture or feeling the woman’s head, and such like. This service was performed for a mere $10 fee. Oh yes, did I mention you get a money-back guarantee?! So, assuming that you wish to subscribe to this service and send in a picture with a $10 check, what is the expected payoff of the swami’s predictions, assuming she actually keeps her word of sending back your money should the prediction prove wrong?
- E(x) = Σx • P(x) = 10 (.5) – .32(.5) = $4.84 including the stamp

