In situations when the two datasets are dependent on each other, the two-sample t-test with dependent means is used. This test is also known as the paired observations test, which means that the number of observations in each of the two datasets has to be the same (n = n1 = n2). For example, if the researcher is interested in testing the before- and after-effects on the productivity of the same sample of employees after a change in work hours, the data is obtained from the same dataset (i.e., the same employees are tested).
The dependent means test uses:
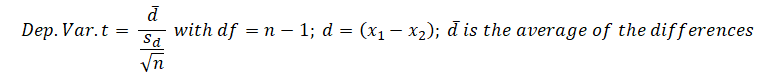
Figure 9.7 provides an example of the productivity study where X1 measured after the change in work hours, compared to the before-change measured in X2. The numbers indicate the total hours it takes to complete a certain activity, and each row of the dataset represents an individual. The hypotheses tested are the typical one-tail test:
H0: μ1 ≥ μ2that is, the two samples’ means are statistically similar
Ha: μ1 < μ2 that is, the two samples’ means are statistically significantly different
As the one-tail p-value calculated is 0.0141, we reject the null hypothesis and accept the alternate hypothesis and conclude that the change in work hours will result in higher productivity (measured by lower total hours required to complete some prespecified task). Figure 9.8 illustrates the implementation of the problem in ROV BizStats.
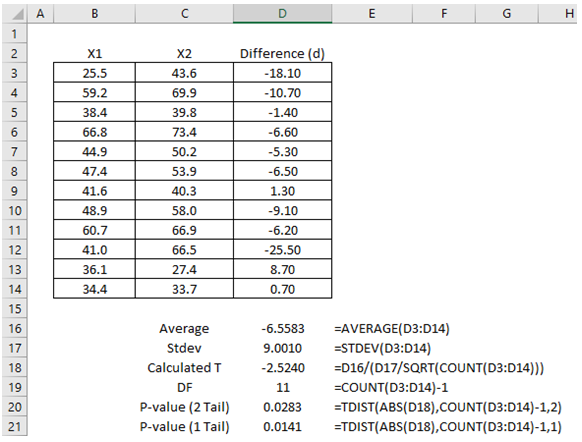
Figure 9.7: Calculations for Dependent Paired Observations T-Test
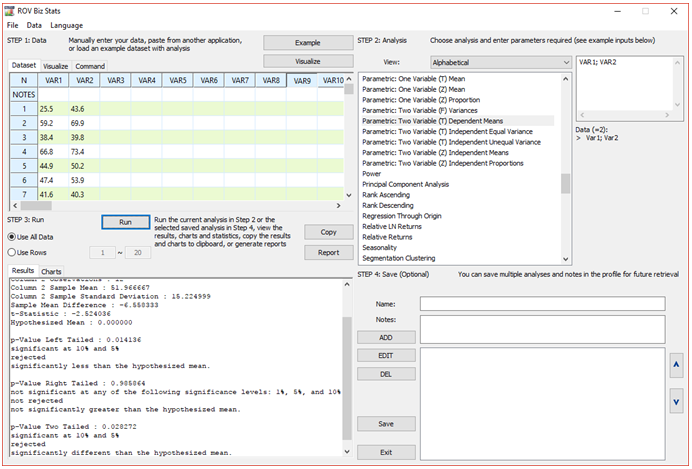
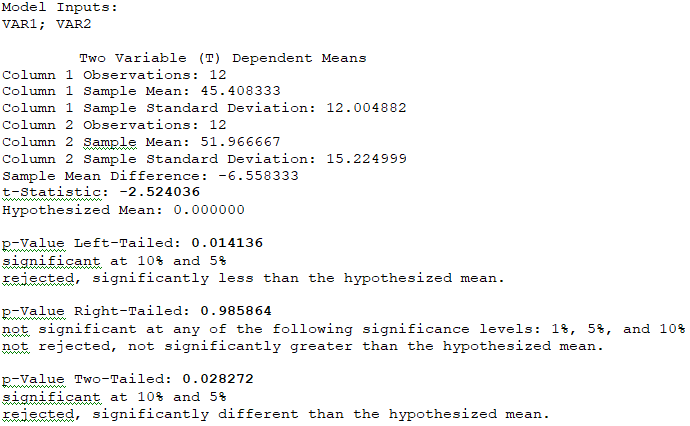
Figure 9.8: Dependent Paired T-Test in ROV BizStats
Extensions of the T-tests
T-tests are pairwise, where we test two variables at once. However, doing multiple t-tests or looking at running all possible combinations of t-tests simultaneously can potentially cause a degree of freedom issue. In other words, you may run into a data mining trap, where you try all possible combinations without regard to a priori or prior theory and knowledge. To circumvent the data mining issue, the Bonferroni test and Hotelling T-Square test provide a simultaneous test that adjusts for the number of tests run.
- Bonferroni Test(Two Variables with Repetition). The Bonferroni Test is an adjustment made to p-values when multiple dependent or independent statistical T-tests are being performed simultaneously on a single dataset. Simultaneous confidence intervals are computed and compared against multiple individual tests. This two-variable with repetition corrections test is applied on two groups of multiple variables each. The null hypothesis tested is that the individual expected differences are all equal to zero.
- Hotelling T-Square: 2 VAR Dependent Pair with Related Measures. The Hotelling T-Square Two Paired Group Test for two sample sets of multiple related features (variables). For example, data on features such as usefulness, attractiveness, durability, and interest level on two new products are collected and listed as column variables. The null hypothesis tested is that there is zero difference between all the related features (variables) compared across the two groups against their respective goals. The Hotelling T-Square for Two Dependent Variables with Related Measures is an extension of the T-Test for Dependent Variables and Bonferroni adjustments applied simultaneously to multiple paired variables.

