Sometimes, the decision variables are not continuous but discrete integers (e.g., 1, 2, 3) or binary (e.g., 0 and 1). We can use such binary decision variables as on-off switches or go/no-go decisions. Figure 17.4 illustrates a project selection model where there are 12 projects listed. The example here uses the file found in Risk Simulator | Example Models | 12 Optimization Discrete. Each project like before, has its own returns (ENPV and NPV for expanded net present value and net present value—the ENPV is simply the NPV plus any strategic real options values), costs of implementation, risks, and so forth. If required, this model can be modified to include required full-time equivalences (FTE) and other resources of various functions, and additional constraints can be set on these additional resources. The inputs into this model are typically linked from other spreadsheet models. For instance, each project will have its own discounted cash flow or returns on investment model. The application here is to maximize the portfolio’s Sharpe Ratio subject to some budget allocation. Many other versions of this model can be created, for instance, maximizing the portfolio returns, or minimizing the risks, or add additional constraints where the total number of projects chosen cannot exceed 6, and so forth, and so on. All of these items can be run using this existing model.
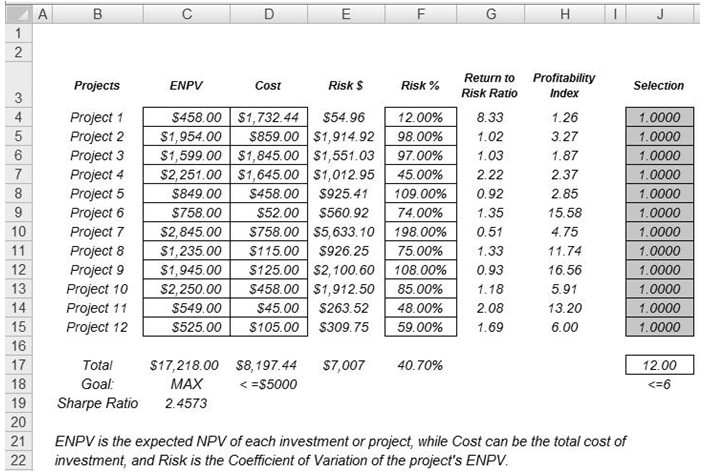
Figure 17.4: Discrete Integer Optimization Model
Procedure
- Open the example file at Risk Simulator | Example Models | 12 Discrete Optimization and start a new profile by clicking on Risk Simulator | New Profile and provide it a name.
- The first step in optimization is to set up the decision variables. Set the first decision variable by selecting cell J4, and select Risk Simulator | Optimization | Set Decision, click on the link icon to select the name cell (B4), and select the Binary variable Then, using Risk Simulator Copy, copy this J4 decision variable cell and paste the decision variable to the remaining cells in J5 to J15.
- The second step in optimization is to set the constraint. There are two constraints here, that is, the total budget allocation in the portfolio must be less than $5,000 and the total number of projects must not exceed 6. So, click on Risk Simulator | Optimization | Constraints… and select ADD to add a new constraint. Then, select cell D17 and make it less than or equal (<=) to 5000. Repeat the step by setting cell J17 <= 6.
- The final step in optimization is to set the objective function and start the optimization by selecting cell C19 and selecting Risk Simulator | Optimization | Set Objective and then run the optimization (Risk Simulator | Optimization | Run Optimization) and selecting the optimization of choice (Static Optimization, Dynamic Optimization, or Stochastic Optimization). To get started, select Static Optimization. Check to make sure that the objective cell is C19 and select Maximize. You can now review the decision variables and constraints if required, or click OK to run the static optimization.
Figure 17.5 shows the screenshots of the foregoing procedural steps. You can add simulation assumptions on the model’s ENPV and Risk (columns C and F) and apply the dynamic optimization and stochastic optimization for additional practice.
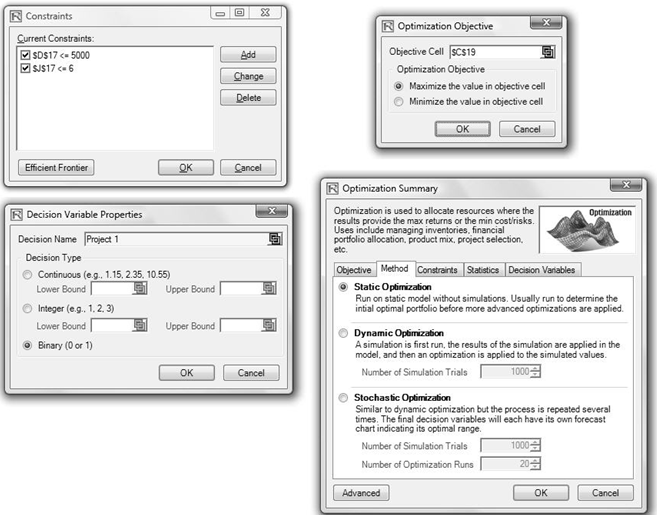
Figure 17.5: Running Discrete Integer Optimization in Risk Simulator
Results Interpretation
Figure 17.6 shows a sample optimal selection of projects that maximizes the Sharpe Ratio. In contrast, one can always maximize total revenues, but as before, this process is trivial and simply involves choosing the highest returning project and going down the list until you run out of money or exceed the budget constraint. Doing so will yield theoretically undesirable projects as the highest yielding projects typically hold higher risks. Now, if desired, you can replicate the optimization using a stochastic or dynamic optimization by adding in assumptions in the ENPV and Risk values.
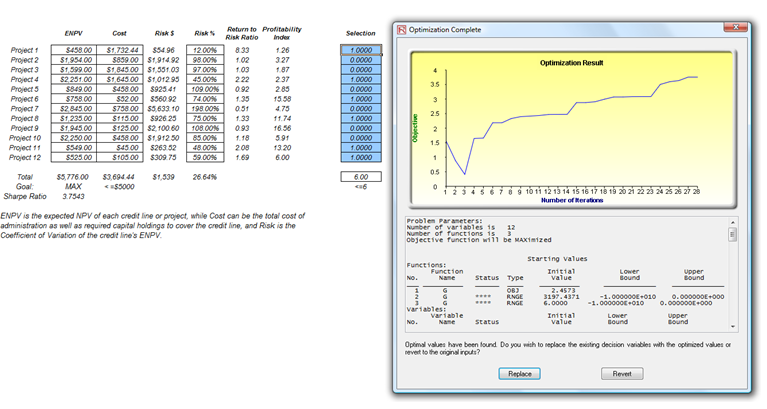
Figure 17.6: Optimal Selection of Projects That Maximizes the Sharpe Ratio

