File Names: Exotic Options – Barrier Option – Up and In, Down and In Double Barrier Call; Exotic Options – Barrier Option – Up and Out, Down and Out Double Barrier Call
Location: Modeling Toolkit | Real Options Models
Brief Description: Computes American and European double barrier options where the option gets kicked in the money or out of the money if the underlying asset or stock breaches an upper or lower barrier
Requirements: Modeling Toolkit, Real Options SLS
The Double Barrier Option is solved using the binomial lattice. This model measures the strategic value of an option (this applies to both calls and puts) that comes either in the money or out of the money when the Asset Value hits either the artificial Upper or Lower Barriers. Therefore, an Up and In and Down and In option (for both calls and puts) indicates that the option becomes live if the asset value hits either the upper or lower barrier. Conversely, for the Up and Out and Down and Out option, the option is live only when neither the upper nor the lower barrier is breached. Examples of this option include contractual agreements whereby if the upper barrier is breached, some event or clause is triggered. The value of barrier options is lower than standard options, as the barrier option will have value within a smaller price range than the standard option. The holder of a barrier option loses some of the traditional option value; therefore, such options should be worth less than a standard option.
Figure 177.1 illustrates an American Up and In, Down and In Double Barrier Option, which is a combination of the Upper and Lower Barrier Options shown previously. Exactly the same logic applies to this Double Barrier Option.
Figure 177.1 illustrates the American Barrier Option solved using the SLS. To change these into a European Barrier Option, set the Intermediate Node Equation to OptionOpen. In addition, for certain types of contractual options, vesting and blackout periods can be imposed. For solving such Bermudan Barrier Options, keep the same Intermediate Node Equation as the American Barrier Options but set the Intermediate Node Equation During Blackout and Vesting Periods to OptionOpen and insert the corresponding blackout and vesting period lattice steps. Finally, if the barrier is a changing target over time, put in several custom variables named Barrier with the different values and starting lattice steps.
Exotic Barrier Options exist when other options are combined with barriers. For instance, an option to expand can be executed only if the PV Asset exceeds some threshold, or a contraction option to outsource manufacturing can only be executed when it falls below some break-even point. Again, such options can be easily modeled using the SLS.
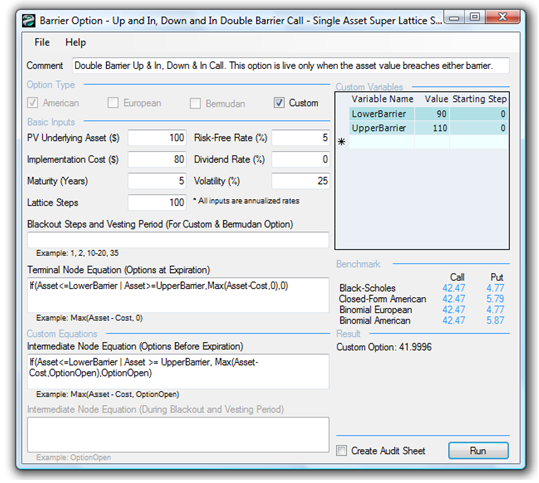
Figure 177.1: Up and in, down and in double barrier option
Exercise: Barrier Options
Barrier options are combinations of call and put options such that they become in the money or out of the money when the asset value breaches an artificial barrier. Standard single upper barrier options can be call up and in, call up and out, put up and in, and put up and out. Standard single lower barrier options can be call down and in, call down and out, put down and in, and put down and out. Double barrier options are combinations of standard single upper and lower barriers.
- Assume that the PV Asset is $200, maturity is 5 years, risk-free rate is 5%, no dividends, and 25% volatility. For each of the barrier option types (upper, lower, and double barrier options), determine:
- What are some examples of nonbinding inputs? That is, show the combinations of cost and barrier levels that make the options nonbinding.
- How do you know the option is nonbinding?
- Show some binding inputs and explain the differences between binding results and nonbinding results.
- Now run the double barrier option, change each input parameter, and explain the effects on the up and in and down and in call option, up and in and down and in put option, up and out and down and out call option, and up and out and down and out put option. Explain your observations when the barrier levels change or when volatility increases.
- Replicate the analysis using a standard lower barrier option.
- Replicate the analysis using a standard upper barrier option.
- Suppose a chemical manufacturer executes sales contracts with a customer and agrees to charge the customer $8/pound of a particular reagent if the customer agrees to purchase 1 million pounds per year for the next 5 years. The market price of the reagent is currently $10/pound. Thus, the customer receives a $2 million discount per year. In addition, if the price is always set at $8/pound, the manufacturer might be losing out on being able to sell products at the higher market prices. Therefore, an agreement is struck whereby the contract holds as long as the market price is below $11/pound. If the prevailing price exceeds this threshold, the product will be sold at this market price. Assume a 25% annualized volatility and a 5% risk-free rate over the next 5 years.
- How much is such a price protection contact worth to the customer if this upper barrier does not exist?
- How much is such a price protection contact worth to the customer if this upper barrier is implemented?
- What happens when the upper threshold is increased?
- What happens when the price volatility of this compound is lower than 25%? Are the price differentials between the option with and without barrier constant for various volatility levels? In other words, is the barrier option a linear function of volatility?

