Theory
Figure 11.3 lists the eight most common time-series models, segregated by seasonality and trend. For instance, if the data variable has no trend or seasonality, then a single moving average model or a single exponential-smoothing model would suffice. However, if seasonality exists but no discernable trend is present, either a seasonal additive or seasonal multiplicative model would be better, and so forth.
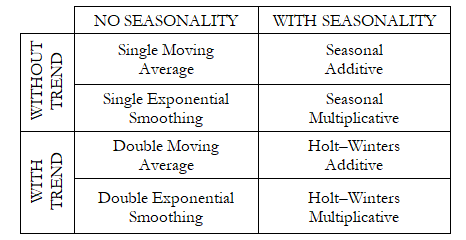
Figure 11.3: The Eight Most Common Time-Series Methods
Procedure
- Start Excel and type in or open an existing spreadsheet with the relevant historical data (the following example uses the Risk Simulator | Example Models | Time-Series Forecasting file).
- Make sure you start a new simulation profile or that there is an existing profile in the model if you want the forecast results to automatically generate Monte Carlo assumptions.
- Select the historical data (do not include the variable name), where the data should be listed in a single column.
- Select Risk Simulator | Forecasting | Time-Series Analysis.
- Choose the model to apply, enter the relevant assumptions, and click OK.
To follow along in this example, choose Auto Model Selection, enter 4 for seasonality periods per cycle, and forecast for 4 periods (Figure 11.4).
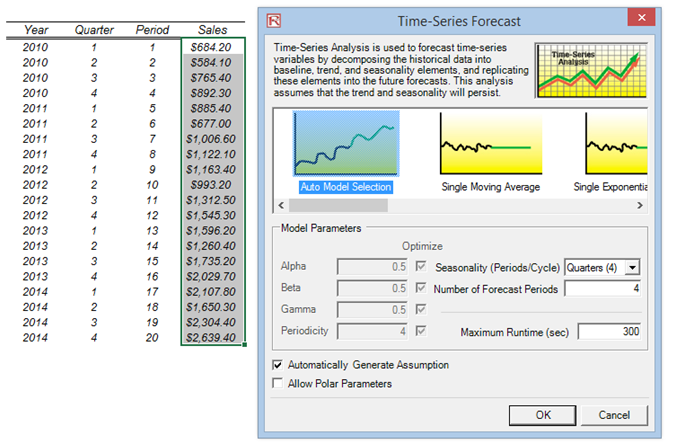
Figure 11.4: Time-Series Analysis
Results Interpretation
Figure 11.5 illustrates the sample results generated by using the Forecasting tool. The model used was a Holt–Winters multiplicative model. Notice that in Figure 11.5, the model-fitting and forecast chart indicate that the trend and seasonality are picked up nicely by the Holt–Winters multiplicative model. The time-series analysis report provides the relevant optimized alpha, beta, and gamma parameters, the error measurements, fitted data, forecast values, and forecast-fitted graph. The parameters are simply for reference. Alpha captures the memory effect of the base level changes over time, beta is the trend parameter that measures the strength of the trend, while gamma measures the seasonality strength of the historical data. The analysis decomposes the historical data into these three elements and then recomposes them to forecast the future. The fitted data illustrate the historical data as well as the fitted data using the recomposed model and show how close the forecasts are in the past (a technique called backcasting). The forecast values are either single-point estimates or assumptions (if the automatically generated assumptions option is chosen and if a simulation profile exists). The graph illustrates the historical, fitted, as well as forecast values. The chart is a powerful communication and visual tool to see how good the forecast model is.
Notes
This time-series analysis module contains the eight time-series models seen in Figure 11.3. You can choose the specific model to run based on the trend and seasonality criteria or choose the Auto Model Selection, which will automatically iterate through all eight methods, optimize the parameters, and find the best-fitting model for your data. Alternatively, if you choose one of the eight models, you can also deselect the optimize checkboxes and enter your own alpha, beta, and gamma parameters. In addition, you will need to enter the relevant seasonality periods if you choose the automatic model selection or any of the seasonal models. The seasonality input must be a positive integer (e.g., if the data is quarterly, enter 4 as the number of seasons or cycles a year, or enter 12 if monthly data or any other positive integer representing the data periods of a full cycle—a drop list preset with these inputs is available or apply the Custom selection to enter in your own positive integer value). Next, enter the number of periods to forecast. This value also has to be a positive integer. The maximum runtime is set at 300 seconds. Typically, no changes are required. However, when forecasting with a significant amount of historical data, the analysis might take slightly longer and if the processing time exceeds this runtime, the process will be terminated. You can also elect to have the forecast automatically generate assumptions; that is, instead of single-point estimates, the forecasts will be assumptions. However, to automatically generate assumptions, a simulation profile must first exist. Finally, the polar parameters option allows you to optimize the alpha, beta, and gamma parameters to include zero and one. Certain forecasting software allows these polar parameters while others do not. Risk Simulator allows you to choose which to use. Typically, there is no need to use polar parameters. In other words, before running a forecast prediction, we first run a backcast, where we test multiple forecast models to determine the one that best fits the historical data. Then, using this selected model, we run internal optimization routines to obtain the required input parameters in the model by minimizing the prediction errors. This methodology, of course, assumes that the best forecast of the future is the past, or that history repeats itself. However, if certain structural shifts and changes are predicted to occur in the near future (e.g., new disruptive technology, acquisition, divestiture, etc.), these shifts can be incorporated into the model after the forecast has been run. See the next chapter for the technical details on time-series forecasting using the eight decomposition methods.
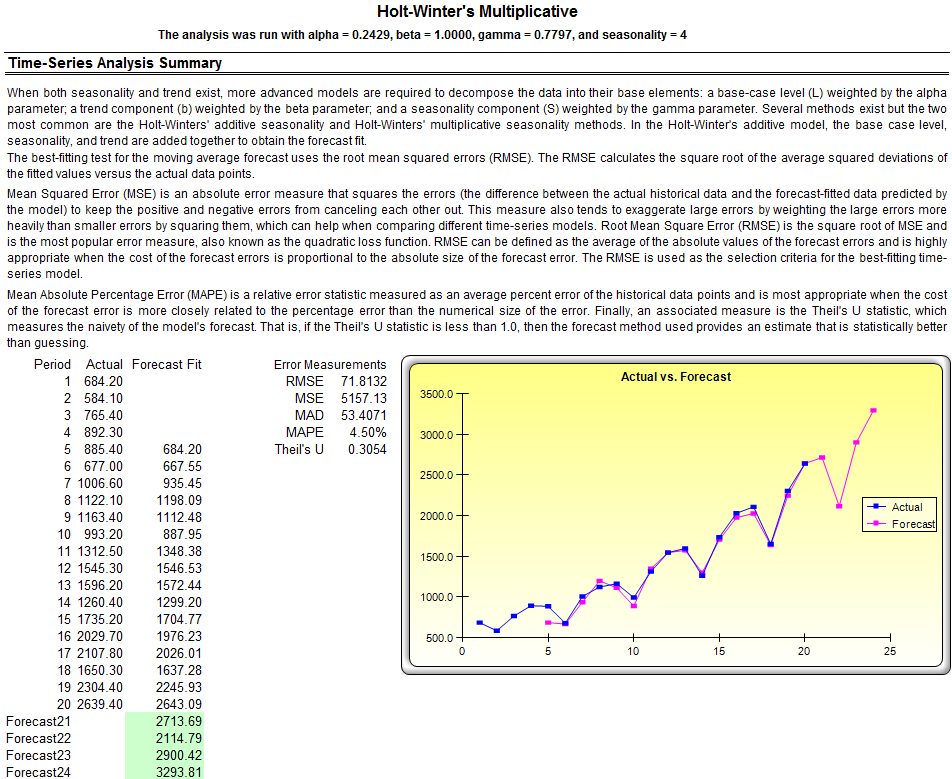
Figure 11.5: Example Holt–Winters Forecast Report

