File Name: Probability of Default – Yields and Spreads
Location: Modeling Toolkit | Prob of Default | Bond Yields and Spreads (Market Comparable)
Brief Description: Generates the probability of default on a bond or debt by looking at market traded instruments’ yields (bond)
Requirements: Modeling Toolkit
Modeling Toolkit Functions Used: MTProbabilityDefaultCumulativeBondYieldApproach, MTProbabilityDefaultHazardRate, MTProbabilityDefaultCumulativeSpreadApproach, MTProbabilityDefaultAdjustedBond-Yield, MTProbabilityDefaultCorrelation, MTProbabilityDefaultAverageDefaults, MTProbabilityDefaultPercentileDefaults
This model looks at the computation of the probability of default on a bond or debt by looking at market-traded instruments. The probability of default measures the degree of likelihood that the borrower of a loan or debt (an obligor) will be unable to make the necessary scheduled repayments on the debt, thereby defaulting on it. If the obligor is unable to pay, the debt is in default, and the lenders have legal avenues to attempt a recovery of the debt or at least partial repayment of the entire debt. The higher the default probability a lender estimates a borrower to have, the higher the interest rate the lender will charge the borrower as compensation for bearing the higher default risk. The probability of default models are categorized as structural or empirical.
Structural models compute the probability of default based on market data (e.g., bond yields and spreads, equity prices, market and book values of assets and liabilities, as well as the volatility of these variables). In contrast, empirical models or credit scoring models are used to quantitatively determine the probability that a loan or loan holder will default, where the loan holder is an individual, by looking at historical portfolios of loans held, where individual characteristics are assessed (e.g., age, educational level, debt to income ratio, etc.).
The bond yield comparable approach is clearly a structural model. In these models, given the annualized spot risk-free yields over time, the corresponding corporate bond yields (both are zero coupon bonds), and the expected recovery rate upon default, we can compute the implied cumulative default probability, the default probability in a particular year, and the hazard rates for each year (Figure 3.1).
In addition, the cumulative default probability between two years can also be computed using the same bond yield approach. Sometimes, only the risky bond or debt’s spread (the premium charged above the risk-free rate) is known. Using this credit spread, the cumulative probability of default can also be determined. To obtain the probability of default in a given year, compute two cumulative default probabilities and get the difference.
This model also exemplifies the use of the Credit Risk Plus method employed by Credit Suisse Financial Products and is used to compute the average number of credit defaults per period given the total number of credit exposures in the portfolio, the cumulative probability of default on average, and the percentile Value at Risk for the portfolio. The Credit Risk Plus method can also be used to compute the percentile given some estimated average number of defaults per period.
The downside to this method is the need for bond yield data that are comparable to the debt or bond to be analyzed. In contrast, the subsequent chapters look at other structural and empirical models that do not require a bond market.
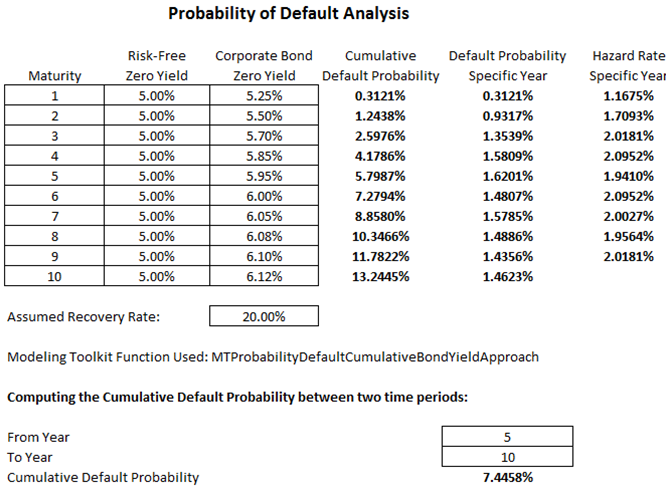

Figure 3.1: Bond Yield Approach to Probability of Default

