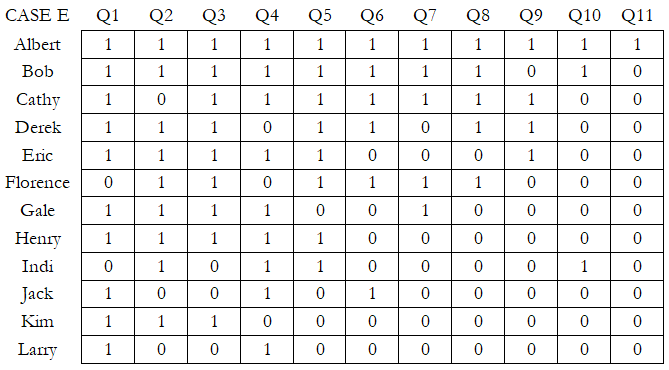
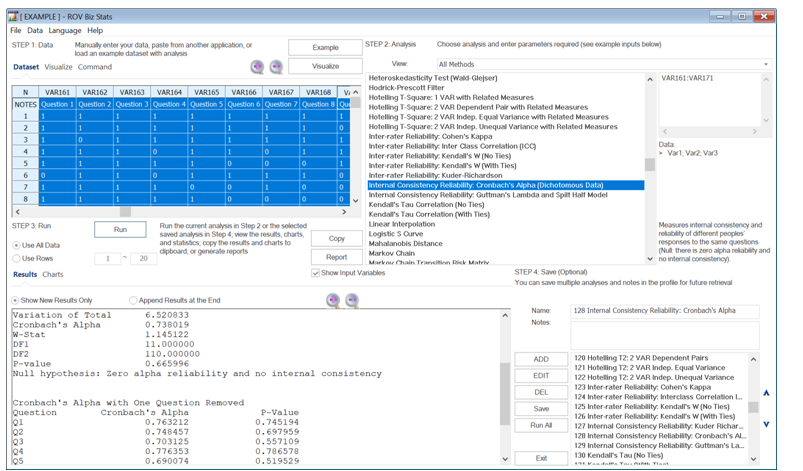
When there exist more than two raters or judges, we can use Cronbach’s Alpha Analysis of Internal Consistency and Reliability. The null hypothesis for Cronbach’s Alpha is that there is zero alpha reliability, and, therefore, there is no internal consistency among the different raters. We see in Case E in the table below, there are 12 respondents to a survey comprising 11 different questions. Note that to run the Cronbach’s Alpha test, the data obtained must be binary. If you look at the data carefully by row, we see that there are respondents such as Albert and Bob who tend to respond with the value 1 regardless of the question, whereas Kim and Larry might do the opposite, with a 0 response. One might even think that some respondents are too lazy to actually answer the questions and will simply fill in the blanks with similar responses throughout. In fact, the calculated Cronbach’s Alpha p-value = 0.6659 in BizStats, which means we cannot reject the null hypothesis and conclude that in Case E, there is no internal consistency among the different respondents. The survey data is, therefore, not consistent, and not reliable.
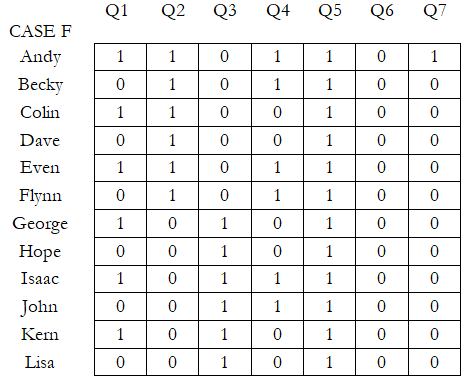
Conversely, in Case F, we see that if you look down each column, there seems to be consistency among all the respondents. For instance, in Questions 6 and 7 (Q6 and Q7), almost all respondents agreed it would be a 0, as opposed to Q5, with all 1s in the column. Q2 and Q3 show that the respondents are equally spread between 0s and 1s. In this Case F, the computed Cronbach’s Alpha p-value = 0.002723 in BizStats, indicating that the null can be rejected, and we conclude that there is, indeed, statistically significant alpha-level reliability among the respondents.