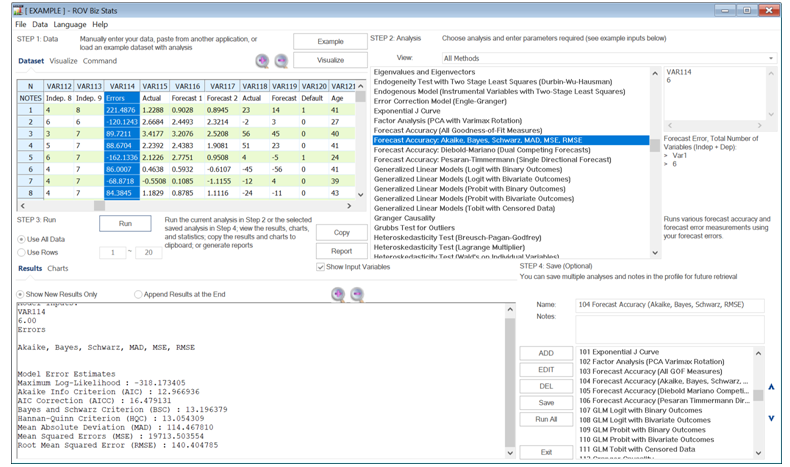
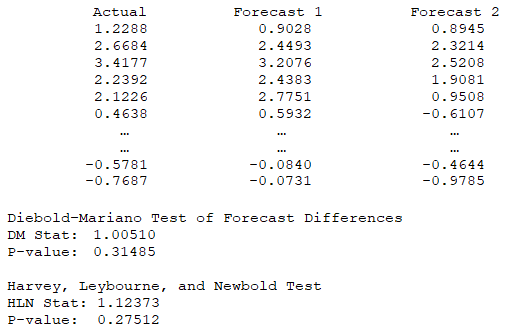
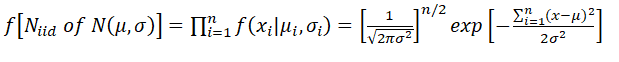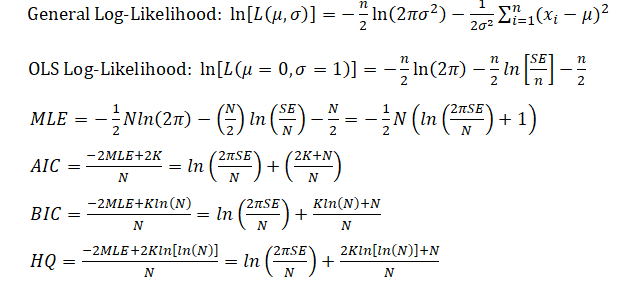Another concept in data and modeling is that of predictability and accuracy. Multiple methods can be used to measure the accuracy of a predictive model. As previously mentioned, in a multivariate regression setting, we can use the R-square, Akaike Information Criterion, Bayes–Schwarz Criterion, and others. As an example, suppose we are comparing between two models’ accuracy. One simple way is to look at the model predicted values and compare them against the historical actuals. The difference would constitute the model’s prediction errors. The following shows two example sets of errors. We can see that model 2’s errors are a lot smaller than model 1’s errors. The computed results using BizStats’ Forecast Accuracy model show that the second model has a lot lower errors and is, therefore, the preferred model with a higher level of accuracy.

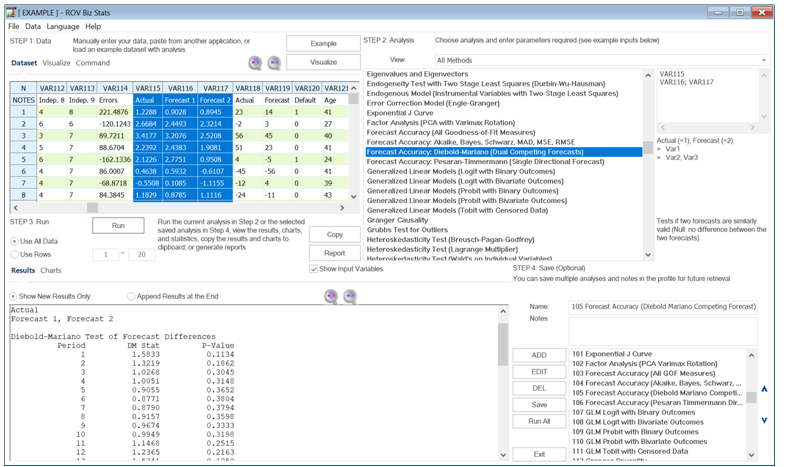
Even if the two models show a different level of forecast accuracy, the next question is whether the two forecasts are statistically significantly different from one another. The Diebold–Mariano Test of Forecast Differences and the Harvey, Leybourne, and Newbold Test allow us to determine if the errors are statistically significant. The null hypothesis tested is that there is no significant difference between the two forecasts.
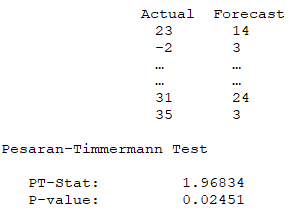
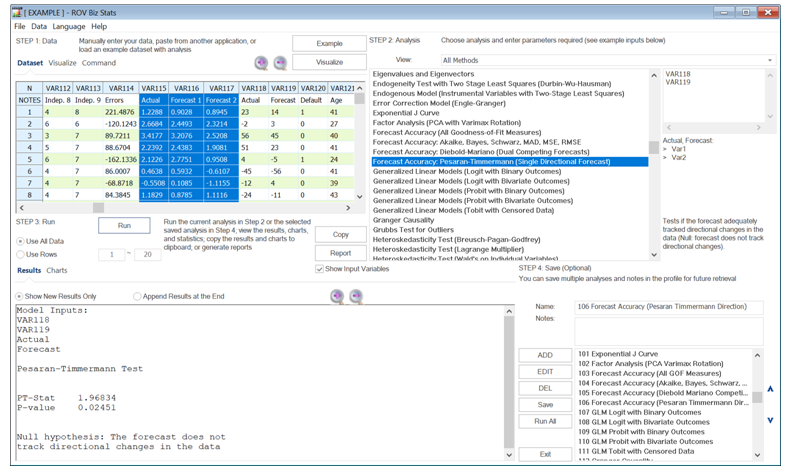
Finally, sometimes the exact forecast accuracy is not in question. Rather, it is the ability to predict directional change that is critical. The Pesaran–Timmerman tests for whether a model can adequately predict and track the directional changes over time. The null hypothesis tested is that the forecast does not track directional changes in the data.
The following provides some insights into how the Akaike Information Criterion (AIC), Bayes Information Criterion (BIC), and Hannan–Quinn (HQ) are derived, using an ordinary least squares (OLS) approach in multiple regression, which assumes that the errors are normally distributed, and the log-likelihood function is maximized (see Chapter 12 for more details on multiple regressions solved using maximum likelihood approaches).
![]()