Theory
One very powerful advanced times-series forecasting tool is the ARIMA or Auto Regressive Integrated Moving Average approach, which assembles three separate tools into a comprehensive model. The first tool segment is the autoregressive or “AR” term, which corresponds to the number of lagged values of the residual in the unconditional forecast model. In essence, the model captures the historical variation of actual data to a forecasting model and uses this variation or residual to create a better predicting model. The second tool segment is the integration order or the “I” term. This integration term corresponds to the number of differencing the time-series data to be forecasted goes through to make the data stationary. This element accounts for any nonlinear growth rates existing in the data. The third tool segment is the moving average or “MA” term, which is essentially the moving average of lagged forecast errors. By incorporating these lagged forecast errors, the model in essence learns from its forecast errors or mistakes and corrects them through a moving average calculation. The ARIMA model follows the Box–Jenkins methodology with each term representing steps taken in the model construction until only random noise remains. Also, ARIMA modeling uses correlation techniques in generating forecasts. ARIMA can be used to model patterns that may not be visible in plotted data. In addition, ARIMA models can be mixed with exogenous variables, but make sure that the exogenous variables have enough data points to cover the additional number of periods to forecast. Finally, be aware that ARIMA cannot and should not be used to forecast stochastic processes or time-series data that are stochastic in nature––use the Stochastic Process module to forecast instead.
There are many reasons why an ARIMA model is superior to usual time-series analysis and multivariate regressions. The common finding in time series analysis and multivariate regression is that the error residuals are correlated with their own lagged values. This autocorrelation violates the standard assumption of regression theory that disturbances are not correlated with other disturbances. The primary problems associated with serial correlation are:
- Regression analysis and basic time-series analysis are no longer efficient among the different linear However, as the error residuals can help to predict current error residuals, we can take advantage of this information to form a better prediction of the dependent variable using ARIMA.
- Standard error computed using the regression and time-series formula is not correct and is generally understated. If there are lagged dependent variables set as the regressors, regression estimates are biased and inconsistent but can be fixed using ARIMA.
Autoregressive Integrated Moving Average or ARIMA(p,d,q) models are the extensions of the AR model that uses three components for modeling the serial correlation in the time series data. The first component is the autoregressive (AR) term. The AR(p) model uses the p lags of the time series in the equation. An AR(p) model has the form:![]() The second component is the integration (d) order term. Each integration order corresponds to differencing the time series. I(1) means differencing the data once. I(d) means differencing the data d times. The third component is the moving average (MA) term. The MA(q) model uses the q lags of the forecast errors to improve the forecast. An MA(q) model has the form:
The second component is the integration (d) order term. Each integration order corresponds to differencing the time series. I(1) means differencing the data once. I(d) means differencing the data d times. The third component is the moving average (MA) term. The MA(q) model uses the q lags of the forecast errors to improve the forecast. An MA(q) model has the form:![]() Finally, an ARMA(p,q) model has the combined form:
Finally, an ARMA(p,q) model has the combined form:![]()
Procedure
- Start Excel and enter your data or open an existing worksheet with historical data to forecast (the illustration shown next uses the example file in Risk Simulator | Example Models | 21 Time-Series Forecasting).
- Click on Risk Simulator | Forecasting | ARIMA and select the time-series data.
- Enter the relevant P, D, and Q parameters (positive integers only, example: 1, 0, 1) and enter the number of forecast periods desired and click OK.
Results Interpretation
In interpreting the results of an ARIMA model, most of the specifications are identical to the multivariate regression analysis (see the chapter on Using the Past to Predict the Future, for more technical details about interpreting the multivariate regression analysis and ARIMA models). However, there are several additional sets of results specific to the ARIMA analysis as seen in Figure 11.13. The first is the addition of Akaike Information Criterion (AIC) and Schwarz Criterion (SC), which are often used in ARIMA model selection and identification. That is, AIC and SC are used to determine if a particular model with a specific set of p, d, and q parameters is a good statistical fit. The SC imposes a greater penalty for additional coefficients than the AIC but, generally, the model with the lowest AIC and SC values should be chosen. Finally, an additional set of results called the autocorrelation (AC) and partial autocorrelation (PAC) statistics are provided in the ARIMA report.
For instance, if autocorrelation AC(1) is nonzero, it means that the series is first-order autocorrelated. If AC dies off more or less geometrically with increasing lags, it implies that the series follows a low-order autoregressive process. If AC drops to zero after a small number of lags, it implies that the series follows a low-order moving average process. In contrast, PAC measures the correlation of values that are k periods apart after removing the correlation from the intervening lags. If the pattern of autocorrelation can be captured by an autoregression of order less than k, then the partial autocorrelation at lag k will be close to zero. The Ljung–Box Q-statistics and their p-values at lag k are also provided, where the null hypothesis being tested is such that there is no autocorrelation up to order k. The dotted lines in the plots of the autocorrelations are the approximate two standard error bounds. If the autocorrelation is within these bounds, it is not significantly different from zero at approximately the 5% significance level. Finding the right ARIMA model takes practice and experience. These AC, PAC, SC, and AIC are highly useful diagnostic tools to help identify the correct model specification. Finally, the ARIMA parameter results are obtained using sophisticated optimization and iterative algorithms, which means that although the functional forms look like those of multivariate regression, they are not the same. ARIMA is a much more computationally intensive and advanced econometric approach.

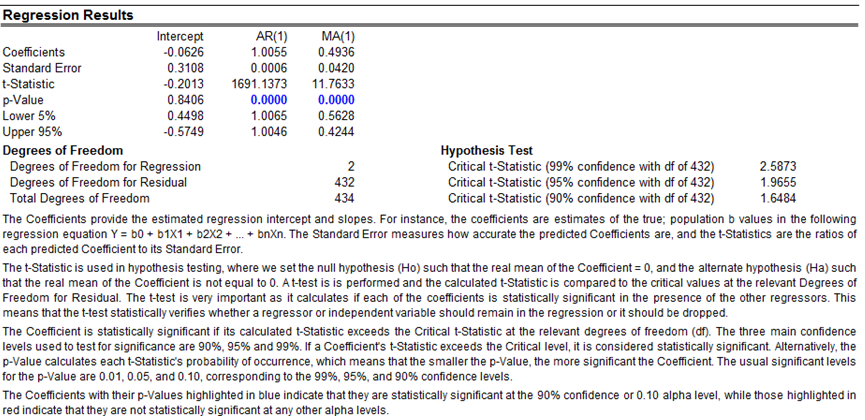
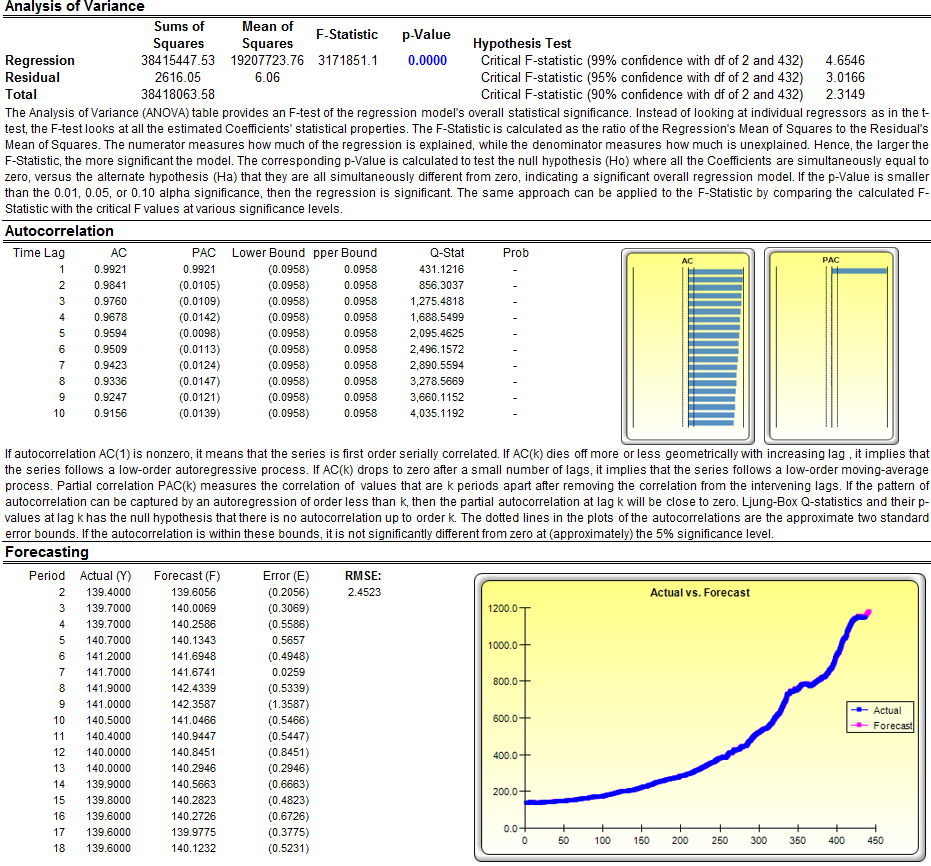
Figure 11.13: Box–Jenkins ARIMA Forecast Report

