File Name: Risk Hedging – Delta Gamma Hedge
Location: Modeling Toolkit | Risk Hedging | Delta Gamma Hedge
Brief Description: Sets up a delta-gamma riskless and costless hedge in determining the number of call options to sell and buy, the number of common stocks to buy, and the borrowing amount required to set up a perfect arbitrage-free hedge
Requirements: Modeling Toolkit
Modeling Toolkit Functions Used: MTDeltaGammaHedgeCallSold, MTDeltaGammaHedgeSharesBought, MTDeltaGammaHedgeMoneyBorrowed
The delta-gamma hedge provides a hedge against larger changes in the asset value. This is done by buying some equity shares and a call option, which are funded by borrowing some amount of money and selling a call option at a different strike price. The net amount is a zero sum game, making this hedge completely effective in generating a zero delta and zero gamma for the portfolio, just as in a delta hedge, where the total portfolio’s delta is zero (e.g., to offset a positive delta of some underlying assets, call options are sold to generate sufficient negative delta to completely offset the existing deltas to generate a zero delta portfolio). The problem with delta-neutral portfolios is that secondary changes (i.e., larger shocks) are not hedged. Delta-gamma hedged portfolios, on the contrary, hedge both delta and gamma risk, making them a lot more expensive to generate. The typical problem with such a hedging vehicle is that in larger quantities, buying and selling additional options or underlying assets may change the market value and prices of the same instruments used to perform the hedge. Therefore, typically, a dynamic hedge or continuously changing hedge portfolios might be required.
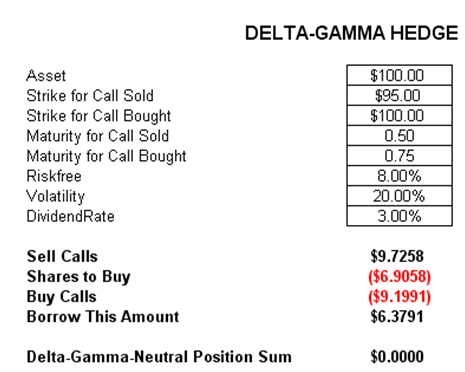
Figure 124.1: Delta-gamma hedging

