File Name: Optimization – Stochastic Portfolio Allocation
Location: Modeling Toolkit | Optimization | Stochastic Portfolio Allocation
Brief Description: Illustrates how to run a stochastic optimization on continuous decision variables with simulation and interpret optimization results
Requirements: Modeling Toolkit, Risk Simulator
This model shows four asset classes with different risk and return characteristics. The idea here is to find the best portfolio allocation such that the portfolio’s bang for the buck or returns to risk ratio is maximized. That is, the goal is to allocate 100% of an individual’s investment among several different asset classes (e.g., different types of mutual funds or investment styles: growth, value, aggressive growth, income, global, index, contrarian, momentum, etc.). This model is different from others in that there exist several simulation assumptions (risk and return values for each asset), as seen in Figure 104.1.
A simulation is run, then optimization is executed, and the entire process is repeated multiple times to obtain distributions of each decision variable. The entire analysis can be automated using Stochastic Optimization.
In order to run an optimization, several key specifications on the model have to be identified first:
Objective: Maximize Return to Risk Ratio (C12)
Decision Variables: Allocation Weights (E6:E9)
Restrictions on Decision Variables: Minimum and Maximum Required (F6:G9)
Constraints: Portfolio Total Allocation Weights 100% (E11 is set to 100%)
Simulation Assumptions: Return and Risk Values (C6:D9)
The model shows the various asset classes. Each asset class has its own set of annualized returns and annualized volatilities. These return and risk measures are annualized values such that they can be consistently compared across different asset classes. Returns are computed using the geometric average of the relative returns, while the risks are computed using the logarithmic relative stock returns approach.
Column E, Allocation Weights, holds the decision variables, which are the variables that need to be tweaked and tested such that the total weight is constrained at 100% (cell E11). Typically, to start the optimization, we will set these cells to a uniform value. In this case, cells E6 to E9 are set at 25% each. In addition, each decision variable may have specific restrictions in its allowed range. In this example, the lower and upper allocations allowed are 10% and 40%, as seen in columns F and G. This setting means that each asset class may have its own allocation boundaries. 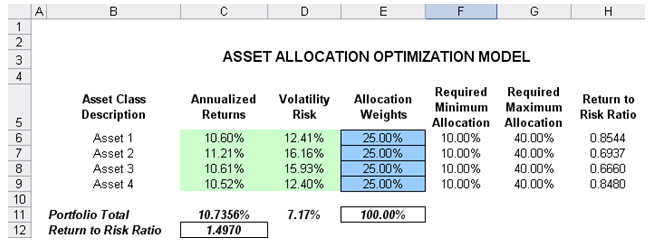
Figure 104.1: Asset allocation model ready for stochastic optimization
Next, column H shows the return to risk ratio, which is simply the return percentage divided by the risk percentage for each asset, where the higher this value, the higher the bang for the buck. The remaining parts of the model show the individual asset class rankings by returns, risk, return to risk ratio, and allocation. In other words, these rankings show at a glance which asset class has the lowest risk, or the highest return, and so forth.
Running an Optimization
To run this model, simply click on Risk Simulator | Optimization | Run Optimization. Alternatively, and for practice, you can set up the model using the following steps.
- Start a new profile (Risk Simulator | New Profile).
- For stochastic optimization, set distributional assumptions on the risk and returns for each asset That is, select cell C6 and set an assumption (Risk Simulator | Set Input Assumption), and make your own assumption as required. Repeat for cells C7 to D9.
- Select cell E6 and define the decision variable (Risk Simulator | Optimization | Set Decision or click on the Set Decision D icon) and make it a Continuous Variable, and then link the decision variable’s name and minimum/maximum required to the relevant cells (B6, F6, G6).
- Then use the Risk Simulator copy on cell E6, select cells E7 to E9, and use Risk Simulator’s paste (Risk Simulator | Copy Parameter) and Risk Simulator | Paste Parameter or use the copy and paste icons). Remember not to use Excel’s regular copy and paste functions.
- Next, set up the optimization’s constraints by selecting Risk Simulator | Optimization | Constraints, selecting ADD, and selecting the cell E11, and making it equal 100% (total allocation, and do not forget the % sign).
- Select cell C12, the objective to be maximized, and make it the objective: Risk Simulator | Optimization | Set Objective or click on the O icon.
- Run the optimization by going to Risk Simulator | Optimization | Run Optimization. Review the different tabs to make sure that all the required inputs in steps 2 and 3 are correct. Select Stochastic Optimization and let it run for 500 trials repeated 20 times (Figure 104.2 illustrates these setup steps).
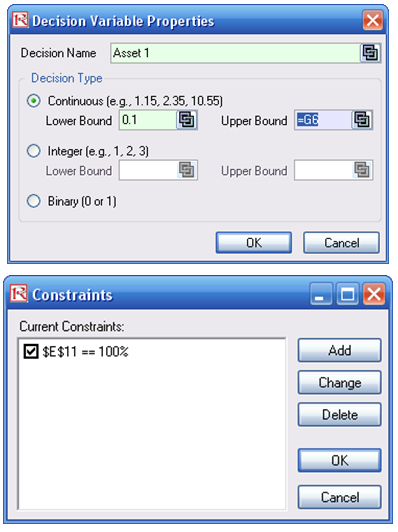
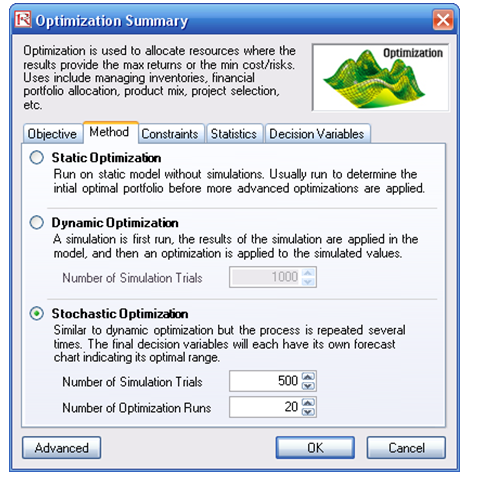
Figure 104.2: Setting up the stochastic optimization problem
Viewing and Interpreting Forecast Results
Stochastic optimization is performed when a simulation is first run and then the optimization is run. Then the whole analysis is repeated multiple times. The result is a distribution of each decision variable rather than a single-point estimate (Figure 104.3). This means that instead of saying you should invest 30.57% in Asset 1, the optimal decision is to invest between 30.10% and 30.99% as long as the total portfolio sums to 100%. This way, the results provide management or decision makers a range of flexibility in the optimal decisions.
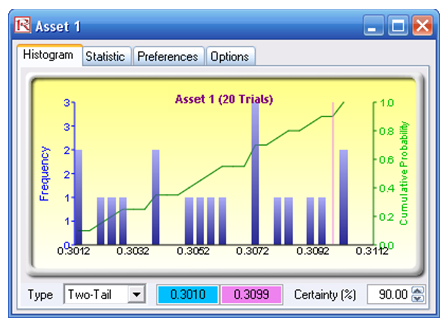
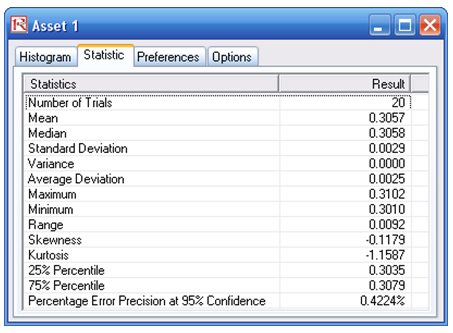
Figure 104.3: Simulated results from the stochastic optimization approach

