File Name: Basic American, European, versus Bermudan Put Options
Location: Modeling Toolkit | Real Options
Brief Description: Compares and values the three different types of option, American (exercisable at any time), Bermudan (exercisable at certain times), and European (exercisable only at expiration), where dividends exist and when dividends do not exist
Requirements: Modeling Toolkit, Real Options SLS
The American and European Put Options without dividends are calculated using the SLS in Figure 179.1. The sample results of this calculation indicate the strategic value of the project’s NPV and provide an option to sell the project within the specified Maturity in years. There is a chance that the project value can significantly exceed the single-point estimate of PV Asset Value (measured by the present value of all uncertain future cash flows discounted at the risk-adjusted rate of return) or be significantly below it. Hence, the option to defer and wait until some of the uncertainty becomes resolved through the passage of time is worth more than executing immediately. The value of being able to wait before executing the option and selling the project at the Implementation Cost in present values is the value of the option. The NPV of executing immediately is simply the Implementation Cost less the Asset Value ($0). The option value of being able to wait and defer selling the asset only if the condition goes bad and becomes optimal is the difference between the calculated results (total strategic value) and the NPV or $24.42 for the American option and $20.68 for the European option. The American put option is worth more than the European put option even when no dividends exist, contrary to the call options seen previously. For simple call options, when no dividends exist, it is never optimal to exercise early. However, sometimes it may be optimal to exercise early for put options, regardless of whether dividend yields exist. In fact, a dividend yield will decrease the value of a call option but increase the value of a put option because when dividends are paid out, the value of the asset decreases. Thus, the call option will be worth less and the put option will be worth more. The higher the dividend yield, the earlier the call option should be exercised and the later the put option should be exercised.
The put option can be solved by setting the Terminal Node Equation as Max(Cost–Asset,0) as seen in Figure 179.1 (example file used: Plain Vanilla Put Option).
Puts have a similar result as calls in that when dividends are included, the basic put option values for American ≥ Bermudan ≥ European in most basic cases. You can confirm this by simply setting the Dividend Rate at 3% and Blackout Steps at 0-80 and rerunning the SLS module.
Recall that a higher dividend means a higher put option value but a lower abandonment option value (see the next chapter on abandonment real options). Thus, a put option is not exactly identical to an abandonment option. A high dividend means the abandonment option’s cost of waiting and holding on to the option is high (e.g., not selling a piece of land means having to pay the taxes, insurance, and maintenance on it, reducing the value of waiting before abandoning). However, for a put option, the asset price or value in the market decreases because of this dividend, making the put option (the ability to sell the asset at a predetermined contractual price) worth more. Dividends in the abandonment option affect the holding cost of the option, but dividends in the put option affect the underlying asset value. Therefore, care has to be taken to choose the relevant option model to use.
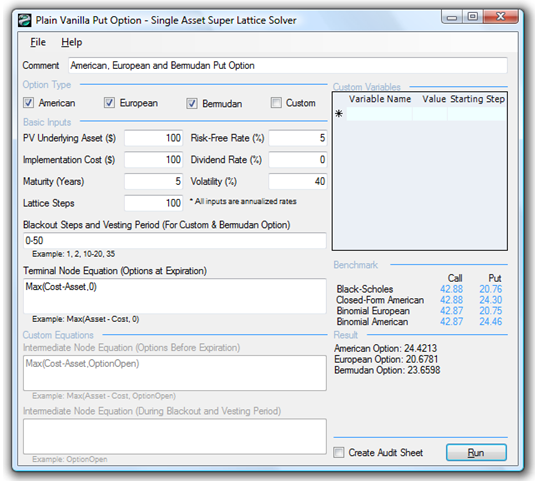
Figure 179.1: American and European put option using SLS
Exercise: American, Bermudan, and European Options
These exercises allow us to compare the results of a European option with American and Bermudan options. In addition, the Black-Scholes model is used to compare the results. The Black-Scholes equation is applicable for analyzing European-type options––that is, options that can be executed only at maturity and not before. The original Black-Scholes model cannot solve an option problem when there are dividend payments. However, extensions of the Black-Scholes model, termed the Generalized Black-Scholes model, can accommodate a continuous dividend payout for a European Option.
Perform the exercises that follow. Assume that a call option’s asset value and strike price are both $100, subject to 25% volatility. The maturity on this option is 5 years, and the corresponding risk-free rate on a similar asset maturity is 5%. Finally, for the Bermudan option, assume a 4-year vesting period.
- Using the Single Asset SLS software, calculate the American, European, and Bermudan call options using a 100-step lattice.
- Compare your results using 5, 10, 50, 100, 300, 500, and 1,000 steps in the SLS software. Explain what happens when the number of steps gets higher.
- Now assume that a continuous dividend payout yielding 3% exists. What happens to the value of the option?
- Show that the value of an American call option is identical to the European call option when no dividends are paid. That is, it is never optimal to execute an American call option early when no dividend payouts exist. Now consider the Bermudan option. What generalities can you come up with?
- Repeat exercise 4 on the put option. Here you will see a very different set of results. What generalities can you come up with?
- Show that as a 3% dividend yield exists, the value of the American call option exceeds the value of a European option. Why is this so? How does the Bermudan option compare? What happens when the blackout steps are significant in the Bermudan option (e.g., increase the vesting period from 4 to 4.5 years and then to 5 years)? What happens when the blackout vesting period is identical to the maturity of the option? How do you model this in the software?
- Repeat exercise 6 on the put option. Here you will see a very different set of results. What generalities can you come up with?

