The Kruskal–Wallis test is the extension of the Wilcoxon Signed-Rank test by comparing more than two independent samples. The corresponding parametric test is the One-Way ANOVA, but unlike the ANOVA, the Kruskal–Wallis does not require that the dataset be randomly sampled from normally distributed populations with equal variances. The Kruskal–Wallis test is a two-tailed hypothesis test where the null hypothesis is such that the population medians of each treatment are statistically identical to the rest of the group; that is, there is no effect among the different treatment groups. Similar to the ANOVA method, the Kruskal–Wallis tests the following hypotheses:
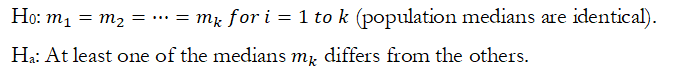
The method starts off with k variables to be tested. For each variable, the data is ranked from smallest to largest, with the smallest value receiving the rank of 1, and all tied ranks are assigned their average values. Then, sum all the ranks for each variable, yielding a list of summed ranks ![]() Then, the H statistic is computed using:
Then, the H statistic is computed using: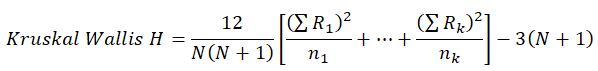
The calculated H is compared to critical H values using a chi-square distribution with df = k-1. Figure 9.36 illustrates the Kruskal–Wallis test. The computed H statistic is over the 10% significance level, so we can reject the null hypothesis at this significance (but not at 5% or 1% significance) and conclude that at least one of the medians is statistically significantly different.
There are two additional nonparametric tests that are equivalent to the parametric ANOVA. For example, the Nonparametric Mood’s Multivariate Median Test is an extension of the Nonparametric Wilcoxon Signed-Rank test for two variables extended to multiple variables. Mood’s test is related to the parametric ANOVA with Multiple Treatments and its Nonparametric Kruskal–Wallis Test equivalence. It uses the same null and alternate hypotheses as in the Kruskal–Wallis test.
In addition, the Nonparametric Cochran’s Q test is for Binary Repeated Measures. It is the nonparametric equivalent of an ANOVA with repeated measures but where the values are binary 0 and 1. The null hypothesis tested is that the proportions of 1s and 0s for all variables are equivalent.
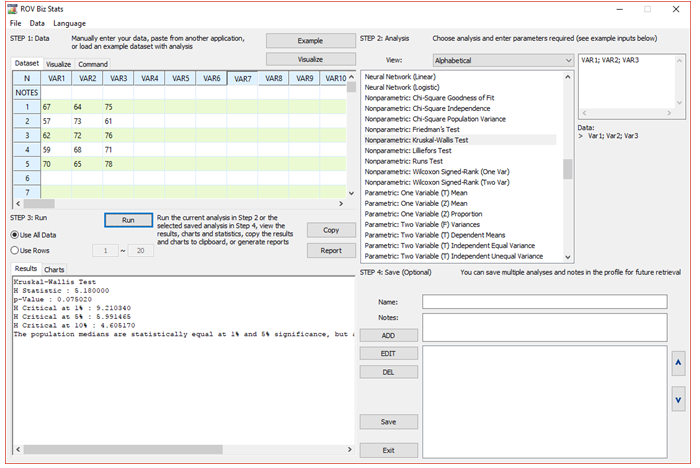
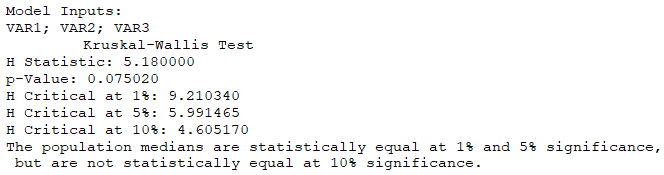
Figure 9.36: Kruskal–Wallis Test

