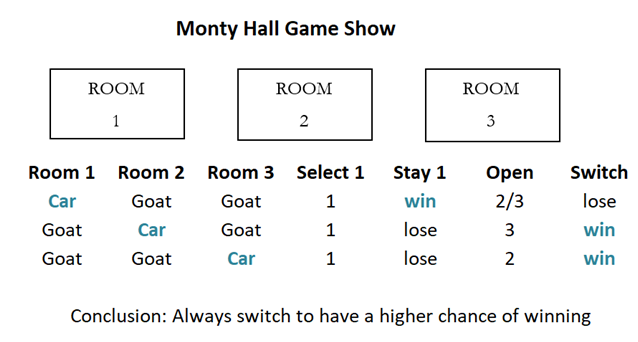
In the final segment of the old Monty Hall television game show, the host, Monty, would show the contestant three closed doors. Behind these doors were three rooms, where one room had a brand new car and the other two a Billy goat each. Clearly, to win the grand prize, the contestant must select the room with the shiny new car. Now, suppose the contestant selects Room 1. Monty then proceeds to the back and sees where the car is actually located. And he then opens a room door that was not previously chosen by the contestant, and which has a goat. Monty then gives the contestant a choice: stay with your current selection or switch to the last remaining room. The question is, should the contestant stay or switch? Which option provides a higher probability of winning?
Let’s use some basic logic on this one. In the figure below, the car can be in any of the rooms and the other two rooms will be the goats. Now, suppose Room 1 was selected, and if the car is in Room 1, then staying will win and switching will lose the car. Score one for staying. In this case, Monty will open either Room 2 or Room 3 as both have Billy goats. However, if the car is in Room 2, Monte has no choice but to open Room 3 because Room 2 has the car and the contestant has already selected Room 1. Hence, switching will guarantee a win as the only room the contestant can switch to is Room 2. The same happens when the car is in Room 3, where Monty has no choice but to open Room 2, and, hence, if the switch is made, only Room 3 can be selected and it is a win. Therefore, there is a 2/3 probability of winning if the contestant switches and 1/3 if the contestant stays put.