File Names: Exotic Options – Barrier Option – Down and In Lower Barrier Call; Exotic Options – Barrier Option – Down and Out Lower Barrier Call
Location: Modeling Toolkit | Real Options
Brief Description: Computes upper barrier options, that is, options that either get kicked in the money or out of the money when they breach a lower barrier
Requirements: Modeling Toolkit, Real Options SLS
The Lower Barrier Option measures the strategic value of an option (this applies to both calls and puts) that comes either in the money or out of the money when the Asset Value hits an artificial Lower Barrier that is currently lower than the asset value. Therefore, a Down and In option (for both calls and puts) becomes live if the asset value hits the lower barrier. Conversely, a Down and Out option is live only when the lower barrier is not breached.
Examples of this option include contractual agreements whereby if the lower barrier is breached, some event or clause is triggered. The value of a barrier option is lower than standard options, as the barrier option will be valuable only within a smaller price range than the standard option. The holder of a barrier option loses some of the traditional option value, and therefore a barrier option should sell at a lower price than a standard option. An example would be a contractual agreement whereby the writer of the contract can get into or out of certain obligations if the asset or project value breaches a barrier.
Figure 175.1 shows a Lower Barrier Option for a Down and In Call. Notice that the value is only $7.3917, much lower than a regular American call option of $42.47. This is because the barrier is set low, at $90. This means that all of the upside potential that the regular call option can have will be reduced significantly, and the option can be exercised only if the asset value falls below this lower barrier of $90 (example file used: Barrier Option – Down and In Lower Barrier Call). To make such a Lower Barrier option binding, the lower barrier level must be below the starting asset value but above the implementation cost. If the barrier level is above the starting asset value, it becomes an upper barrier option. If the lower barrier is below the implementation cost, the option will be worthless under all conditions. When the lower barrier level is between the implementation cost and starting asset value, the option is potentially worth something. However, the value of the option is dependent on volatility. Using the same parameters as in Figure 175.1 and changing the volatility, the following examples illustrate what happens:
- At a volatility of 75%, the option value is $4.34.
- At a volatility of 25%, the option value is $3.14.
- At a volatility of 5%, the option value is $0.01.
The lower the volatility, the lower the probability that the asset value will fluctuate enough to breach the lower barrier such that the option will be executed. By balancing volatility with the threshold lower barrier, you can create optimal trigger values for barriers.
Figure 175.2 shows the Lower Barrier Option for Down and Out Call option. Here, if the asset value breaches this lower barrier, the option is worthless; it is valuable only when it does not breach this lower barrier. As call options have higher values when the asset value is high, and lower values when the asset value is low, this Lower Barrier Down and Out Call Option is worth almost the same as the regular American option. The higher the barrier, the lower the value of the lower barrier option will be (example file used here is the Barrier Option – Down and Out Lower Barrier Call). For instance,
- At a lower barrier of $90, the option value is $42.19
- At a lower barrier of $100, the option value is $41.58
Figures 175.1 and 175.2 illustrate American Barrier Options. To change these into European Barrier Options, set the Intermediate Node Equation to OptionOpen. In addition, for certain types of contractual options, vesting and blackout periods can be imposed. For solving such Bermudan Barrier Options, keep the same Intermediate Node Equation as the American Barrier Options but set the Intermediate Node Equation During Blackout and Vesting Periods to OptionOpen and insert the corresponding blackout and vesting period lattice steps. Finally, if the barrier is a changing target over time, put in several custom variables named Barrier with the different values and starting lattice steps.
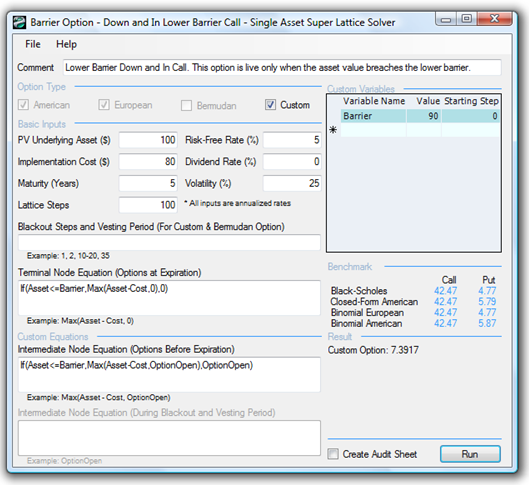
Figure 175.1: Down and in lower American barrier option
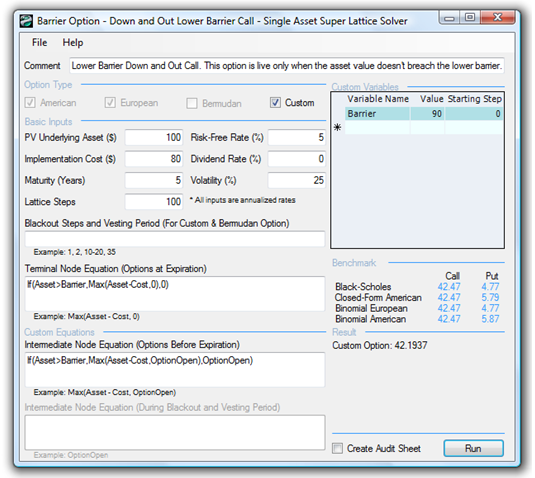
Figure 175.2: Down and out lower American barrier option

