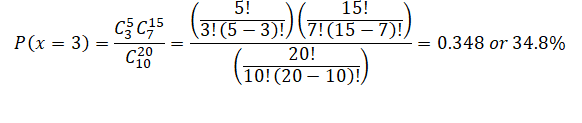The hypergeometric distribution is similar to the binomial distribution in that both describe the number of times a particular event occurs in a fixed number of trials. The difference is that binomial distribution trials are independent, whereas hypergeometric distribution trials change the probability for each subsequent trial and are called trials without replacement. For example, suppose a box of manufactured parts is known to contain some defective parts. You choose apart from the box, find it is defective, and remove the part from the box. If you choose another part from the box, the probability that it is defective is somewhat lower than for the first part because you have removed a defective part. If you had replaced the defective part, the probabilities would have remained the same, and the process would have satisfied the conditions for a binomial distribution.
The three conditions underlying the hypergeometric distribution are:
- The total number of items or elements (the population size) is a fixed number, a finite population. The population size must be less than or equal to 1,750.
- The sample size (the number of trials) represents a portion of the population.
- The known initial probability of success in the population changes after each trial.
The mathematical constructs for the hypergeometric distribution are as follows:
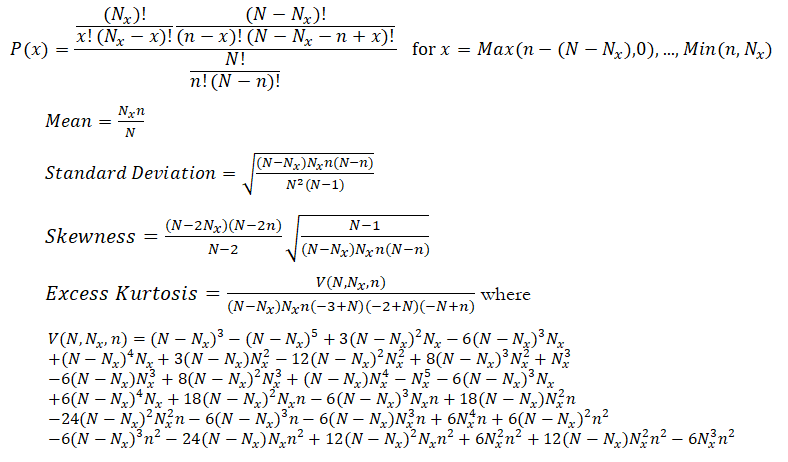 The number of items in the population (N), trials sampled (n), and number of items in the population that have the successful trait (Nx) are the distributional parameters. The number of successful trials is denoted x.
The number of items in the population (N), trials sampled (n), and number of items in the population that have the successful trait (Nx) are the distributional parameters. The number of successful trials is denoted x.
Input requirements:
Population ≥ 2 and integer
Trials > 0 and integer
Successes > 0 and integer
Population > Successes
Trials < Population
Population < 1750
To reiterate, for a hypergeometric distribution:
- Dependent probabilities are acceptable.
- As n increases, the hypergeometric distribution approaches the binomial distribution.
- Use the hypergeometric distribution when n/N ≥ 0.05, or when there are other statistical dependencies, or when there is a complex selection of samples from a given population.
- Sampling without replacement is assumed.
- It is a more complex combination counting rule compared to a simpler combinatorial rule in the binomial distribution.
Example: Of a group of 20 Ph.Ds. in Statistics, we know that 5 of them are highly competent and the others had rich parents who donated to the school heavily and are incompetent. What is the probability that of 10 randomly selected, 3 are highly competent?