File Name: Debt Analysis – Cox Model on Price and Yield of Risky Debt with Mean-Reverting Rates
Location: Modeling Toolkit | Debt Analysis | Cox Model on Price and Yield of Risky Debt with Mean-Reverting Rates
Brief Description: Applies the Cox model to price risky debt as well as to model the yield curve, assuming that interest rates are stochastic and follow mean-reverting rates
Requirements: Modeling Toolkit, Risk Simulator
Modeling Toolkit Functions Used: MTCIRBondPrice, MTCIRBondYield
The Cox-Ingersoll-Ross (CIR) stochastic model of mean-reverting interest rates is modeled here to determine the value of a zero-coupon bond and to reconstruct the yield curve (term structure of interest rates). This model assumes a stochastic and mean-reverting term structure of interest rates with a rate of reversion as well as the long-run rate that the interest reverts to in time. A Yield Curve CIR model shown in a later chapter is used to generate the yield curve and term structure of interest rates using this CIR model (Figure 17.1).
Such mean-reverting models imply that the underlying asset (bond or debt) is highly susceptible to fluctuations in the prevailing interest rates of the economy. And in order to model the price of these interest-sensitive instruments, the behavior of interest rates will first need to be modeled. Interest rates are assumed to be mean-reverting, that is, there is a long-run mean rate at which short-term interest rates are attracted to, tend to, or revert to, at some rate of mean reversion. For instance, in the United States, the Federal Reserve controls interest rates in the economy (by changing the discount rate at which banks can borrow from the central bank, forcing this rate to permeate throughout the economy; changing the required reserve ratio of bank holdings; or performing some sale or purchase of Treasury securities by the Federal Open Market Commission) in order to control the general inflation rate and economic growth. This means that there is typically a long-term economic growth rate, inflation rate, and, hence, interest rate that the Federal Reserve targets. When rates are too high, they are reduced, and vice versa, which means that interest rates, although stochastic and unpredictable in nature, are not as volatile as one would expect. This mean-reverting dampening effect is modeled here.
Finally, the interest rate volatility can be easily modeled using the Volatility models in the Modeling Toolkit, and the market price of interest rate risk is the same as the market price of risk for equity. It is the prevailing interest rate for a similar type of bond or debt (with the same credit risk structure), less the risk-free rate of similar maturities.
You may also use Risk Simulator to run simulations on the inputs to determine the price and yield of debt, or to determine the input parameters such as the long-run mean rate and rate of mean reversion. Use Risk Simulator’s Statistical Analysis tool to determine these stochastic input parameters when calibrated on historical data. The Forecasting – Data Diagnostics model has examples on how to calibrate these stochastic input parameters based on historical data).
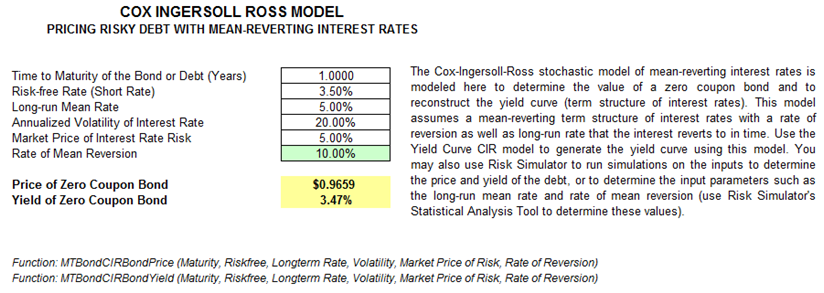
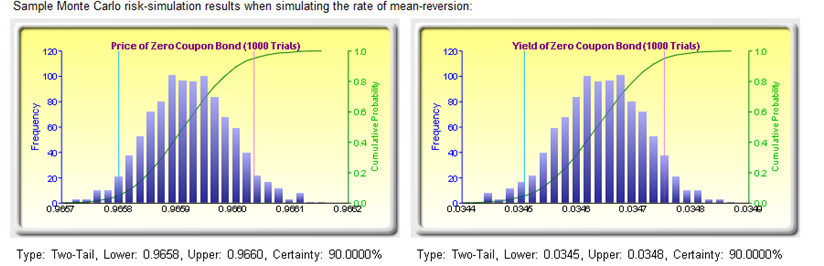
Figure 17.1: Cox model with underlying mean-reverting interest rates

