Apart from the standard multivariate regression and bivariate regressions (and their corresponding functional forms), there are other regression variations and regression-related methods. The following provides a summary of the related models you can run in BizStats.
- Cointegration Test or Engle–Granger Cointegration Test. The Engle–Granger test is used to identify if there exists any cointegration of two nonstationary time-series variables. First of all, the two variables need to be nonstationary, otherwise a simple linear and nonlinear correlation would typically suffice in identifying if there is a co-movement relationship between them. If two time-series variables are nonstationary to order one, I(1), and if a linear combination of these two series is stationary at I(0), then these two variables are, by definition, cointegrated. Many macroeconomic data are I(1), and conventional forecasting and modeling methods do not apply due to the nonstandard properties of unit root I(1) processes. This cointegration test can be applied to identify the presence of cointegration, and if confirmed to exist, a subsequent Error Correction Model can then be used to forecast the time-series variables.
- Cox Regression. The Cox’s proportional hazards model for survival time is used to test the effect of several variables at the time a specified event takes to happen. For example, in medical research, we can use the Cox model to investigate the association between the survival time of patients using one or more predictor variables.
- Discriminate Analysis(Linear and Nonlinear). A discriminant analysis is related to ANOVA and multivariate regression analysis, where it attempts to model one dependent variable as a linear or nonlinear combination of other independent variables. A Discriminant Analysis has continuous independent variables and a categorical dependent variable. Think of the discriminant analysis as a statistical analysis using a linear or nonlinear discriminant function to assign data to one of two or more categories or groups.
- Endogeneity Test with Two-Stage Least Squares (Durbin–Wu–Hausman). This tests if a regressor is endogenous using the two-stage least squares (2SLS) method and applying the Durbin–Wu–Hausman test. A Structural Model and a (2SLS) Reduced Model are both computed in a 2SLS paradigm, and a Hausman test is administered to test if one of the variables is endogenous.
- Endogenous Model (Instrumental Variables with Two-Stage Least Squares). If the regressor is endogenous, we can apply a two-stage least squares (2SLS) with instrumental variables (IV) on a bivariate model to estimate the model.
- Error Correction Model (Engle–Granger). This is also known as an Error Correction Model where we assume that the variables exhibit cointegration. That is, if two time-series variables are nonstationary in the first order, I(1), and when both variables are found to be cointegrated (the I(0) relationship is stationary), we can run an error correction model for estimating short-term and long-term effects of one time-series on another. The error correction comes from previous periods’ deviation from a long-run equilibrium, where the error influences its short-run dynamics.
- Granger Causality. This test is applied to see if one variable Granger causes another variable and vice versa, using restricted autoregressive lags and unrestricted distributive lag models. Predictive causality in finance and economics is tested by measuring the ability to predict the future values of a time series using prior values of another time series. A simpler definition might be that a time-series variable X Granger causes another time-series variable Y if predictions of the value of Y are based solely on its own prior values and on the prior values of X, and these are comparatively better than predictions of Y based solely on its own past values. The causality loop is modeled using these data leads and lags.
- Multiple Poisson Regression (Population and Frequency). The Poisson Regression is like the Logit Regression in that the dependent variables can only take on non-negative values, but also that the underlying distribution of the data is a Poisson distribution, drawn from a known population size.
- Multiple Regression (Deming Regression with Known Variance). In regular multivariate regressions, the dependent variable Y is modeled and predicted by independent variables
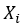 with some error ε. However, in a Deming regression, we further assume that the data collected for Y and X have additional uncertainties and errors, or variances, that are used to provide a more relaxed fit in a Deming model.
with some error ε. However, in a Deming regression, we further assume that the data collected for Y and X have additional uncertainties and errors, or variances, that are used to provide a more relaxed fit in a Deming model. - Multiple Regression (Ordinal Logistic Regression). This model runs a multivariate ordinal logistic regression with two predictor variables and multiple frequencies of ordered variables. For instance, the two categorical variables of Gender (0/1) and Age (1–5), with five variables filled with the numbers or frequencies of people who responded Strongly Agree, Agree, Neutral, Disagree, or Strongly Disagree, which presumable are ordered. Note that this is an ordinal dataset where the Age variable is ordered, and it is multinomial because we are forecasting the frequencies and probabilities of the four count variables.
- Multiple Regression (Through Origin). This model runs a multiple linear regression but without an intercept. This method is used when an intercept may not conceptually or theoretically apply to the data being modeled. As examples, a factory cannot produce outputs if the equipment is not running or the gravitational force of a large object does not exist when there is zero mass.
- Multiple Ridge Regression (Low Variance, High Bias, High VIF). A Ridge Regression model’s results come with a higher bias than an Ordinary Least Squares standard multiple regression but have less variance. It is more suitable in situations with high Variance Inflation Factors and multicollinearity or when there is a high number of variables compared to data points. Clearly, in the case of high VIF with multicollinearity, some of the highly colinear variables will need to be dropped, but for whatever reason these colinear variables need to be included, a ridge-based regression is a better alternative.
- Multiple Weighted Regression for Heteroskedasticity. The Multivariate Regression on Weighted Variables is used to correct for heteroskedasticity in all the variables. The weights used to adjust these variables are the user input standard deviations. Clearly, this method is only applicable for time-series variables, due to the heteroskedastic assumption.
- Stepwise Regression. When there are multiple independent variables vying to be in a multivariate regression model, it can be cumbersome to identify and specify the correct combinations of variables in the model. A stepwise regression can be run to systematically identify which variables are statistically significant and should be inserted into the final model. Several simple algorithms exist for running stepwise regressions:
- Stepwise Regression(Backward). In the backward method, we run a regression with Y on all X variables and, reviewing each variable’s p-value, systematically eliminate the variable with the largest p-value. Then run a regression again, repeating each time until all p-values are statistically significant.
- Stepwise Regression(Correlation). In the correlation method, the dependent variable Y is correlated to all the independent variables X, and starting with the X variable with the highest absolute correlation value, a regression is run. Then subsequent X variables are added until the p-values indicate that the new X variable is no longer statistically significant. This approach is quick and simple but does not account for interactions among variables, and an X variable, when added, will statistically overshadow other variables.
- Stepwise Regression(Forward). In the forward method, we first correlate Y with all X variables, run a regression for Y on the highest absolute value correlation of X, and obtain the fitting errors. Then, correlate these errors with the remaining X variables and choose the highest absolute value correlation among this remaining set and run another regression. Repeat the process until the p-value for the latest X variable coefficient is no longer statistically significant and then stop the process.
- Stepwise Regression(Forward and Backward). In the forward and backward method, apply the forward method to obtain three X variables, and then apply the backward approach to see if one of them needs to be eliminated because it is statistically insignificant. Repeat the forward method and then the backward method until all remaining X variables are considered.

