One powerful automated approach to regression analysis is stepwise regression and, based on its namesake, the regression process proceeds in multiple steps. There are several ways to set up these stepwise algorithms including the correlation approach, forward method, backward method, and the forward and backward method (these methods are all available in Risk Simulator).
In the correlation method, the dependent variable (Y ) is correlated to all the independent variables (X ), and starting with the X variable with the highest absolute correlation value, a regression is run, then subsequent X variables are added until the p-values indicate that the new X variable is no longer statistically significant. This approach is quick and simple but does not account for interactions among variables, and an X variable, when added, will statistically overshadow other variables.
In the forward method, we first correlate Y with all X variables, run a regression for Y on the highest absolute value correlation of X, and obtain the fitting errors. Then, correlate these errors with the remaining X variables and choose the highest absolute value correlation among this remaining set and run another regression. Repeat the process until the p-value for the latest X variable coefficient is no longer statistically significant then stop the process.
In the backward method, run a regression with Y on all X variables and reviewing each variable’s p-value, systematically eliminate the variable with the largest p-value, then run a regression again, repeating each time until all p-values are statistically significant.
In the forward and backward method, apply the forward method to obtain three X variables then apply the backward approach to see if one of them needs to be eliminated because it is statistically insignificant. Then repeat the forward method, and then the backward method until all remaining X variables are considered.
Table 11.1 illustrates the sample results using the same dataset as in the multiple regression model in Figure 11.7. Using the Stepwise Regression: Backward method, we see that the model starts by using all independent variables (Arrangement 1: Y to X1; X2; X3; X4; X5), identifies the least significant variable as X4, and re-runs the second regression model (Arrangement 2: Y to X1; X2; X3; X5). The algorithm then drops variables X1 and X5 in the subsequent two runs. The final result indicates the best-fitting model of Y to X2; X3. This result confirms the multiple regression shown in Figure 11.8, where we see that “Bachelor’s Degree” (VAR1), “Population Density” (VAR4), and “Unemployment Rate” (VAR5) are not significant and should be removed and that the multiple regression should be re-run with only significant variables.
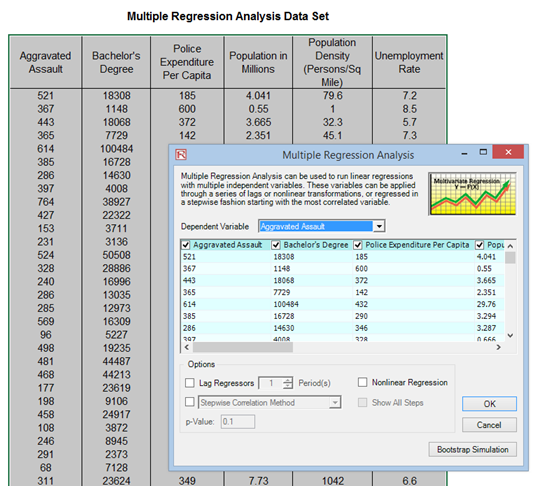
Figure 11.7: Running a Multivariate Regression
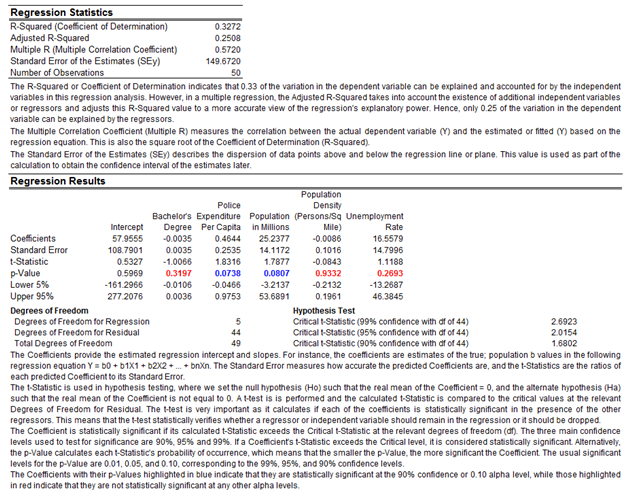
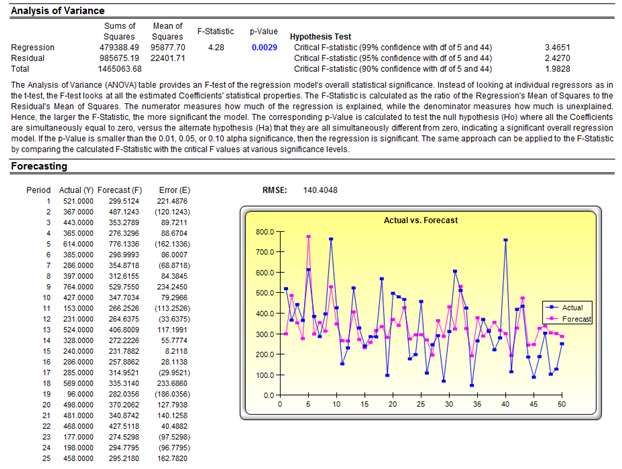
Figure 11.8: Multivariate Regression Results
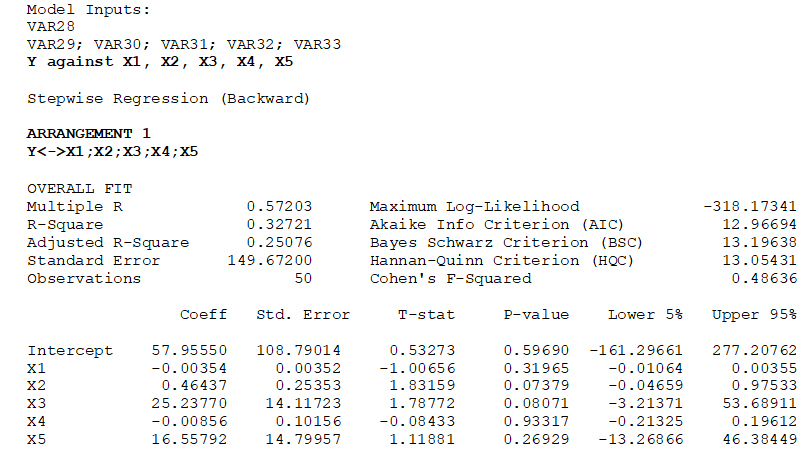
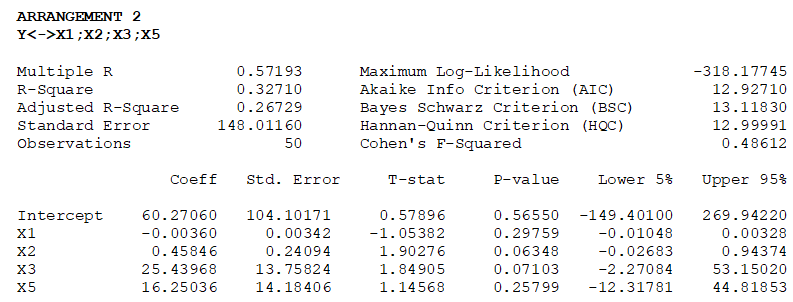
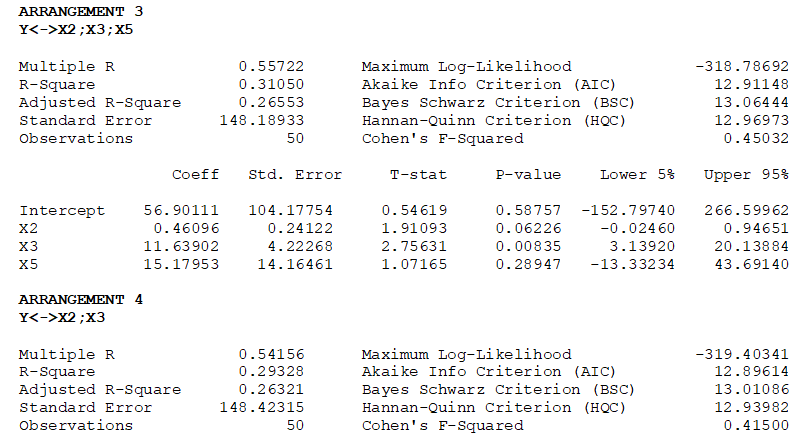

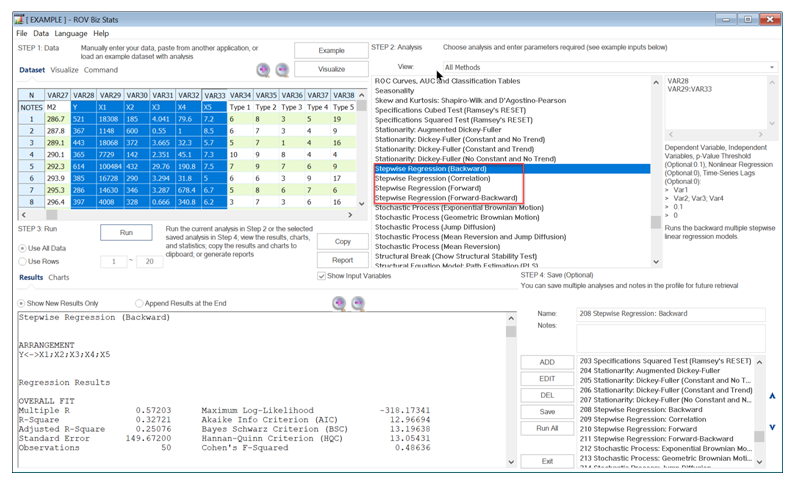
Table 11.1: Stepwise Regression Results

