File Name: Real Options – Simple Calls and Puts Using Trinomial Lattices
Location: Modeling Toolkit | Real Options Models
Brief Description: Solves simple call and put options using trinomial lattices and used to compare with the results from binomial lattices
Requirements: Modeling Toolkit, Real Options SLS
Building and solving trinomial lattices is similar to building and solving binomial lattices, complete with the up/down jumps and risk-neutral probabilities, but it is more complicated due to more branches stemming from each node. At the limit, both the binomial and trinomial lattices yield the same result, as seen in the following table. However, the lattice-building complexity is much higher for trinomial or multinomial lattices. The only reason to use a trinomial lattice is because the level of convergence to the correct option value is achieved more quickly than by using a binomial lattice. In the table below showing the convergence of trinomials and binomials, notice how the trinomial lattice yields the correct option value with fewer steps than it takes for a binomial lattice (1,000 as compared to 5,000). Because both yield identical results at the limit but trinomials are much more difficult to calculate and take a longer computation time, the binomial lattice is usually used instead. However, a trinomial is required when the underlying asset follows a mean-reverting process.
Figure 193.1 shows another example. To run this model, use the SLS software and click on Create a New Multinomial Option Model. The computed American Call is $31.99 using a 5-step trinomial, and is identical to a 10-step binomial lattice seen in Figure 193.2. Therefore, due to the simpler computation and the speed of computation, the SLS software uses binomial lattices instead of trinomials or other multinomial lattices. As noted previously, the only time a trinomial lattice is truly useful is when the underlying asset of the option follows a mean-reversion tendency.
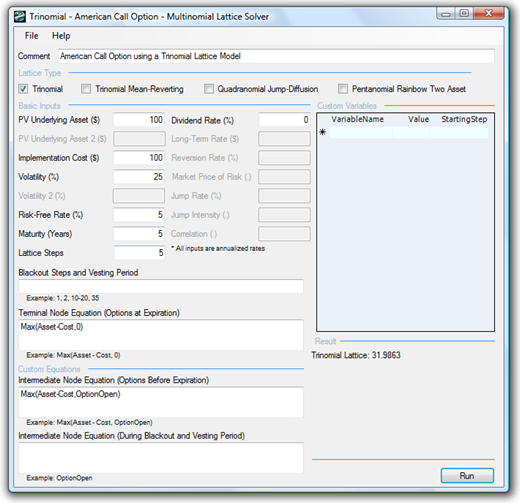
Figure 193.1: Simple trinomial lattice solution
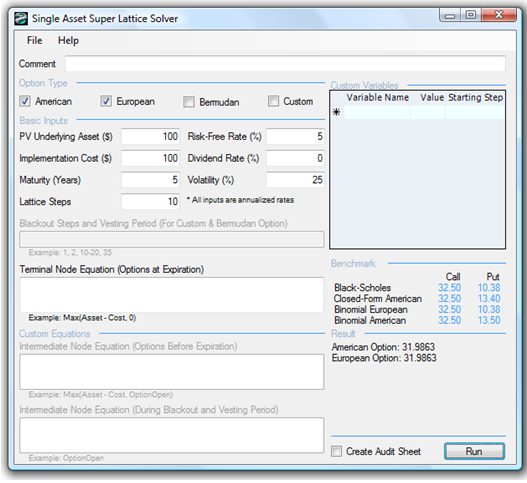
Figure 193.2: 10-step binomial lattice comparison result

