File Name: Real Options – Dual-Asset Rainbow Option Pentanomial Lattice
Location: Modeling Toolkit | Real Options Models
Brief Description: Solves a rainbow option made up of two correlated underlying assets by applying a pentanomial lattice
Requirements: Modeling Toolkit, Real Options SLS
The Dual Asset Rainbow Option for both American and European options requires the Pentanomial Lattice approach. Rainbows on the horizon after a rainy day comprise various colors of the light spectrum, and although rainbow options are not as colorful as their physical counterparts, they get their name from the fact that they have two or more underlying assets rather than one. In contrast to standard options, the value of a rainbow option is determined by the behavior of two or more underlying elements and by the correlation between these underlying elements. That is, the value of a rainbow option is determined by the performance of two or more underlying asset elements. This particular model is appropriate when there are two underlying variables in the option (e.g., Price of Asset and Quantity) where each fluctuates at different rates of volatilities but at the same time might be correlated (Figure 184.1). These two variables are usually correlated in the real world, and the underlying asset value is the product of price and quantity. Due to the different volatilities, a pentanomial or five-branch lattice is used to capture all possible combinations of products (Figure 184.2). Be aware that certain combinations of inputs may yield an unsolvable lattice with negative implied probabilities. If that result occurs, a message will appear. Try a different combination of inputs as well as higher lattice steps to compensate.
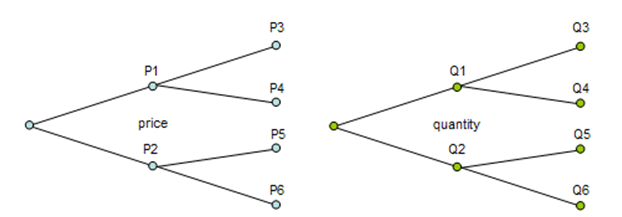
Figure 184.1: Two binomial lattices (asset prices and quantity)
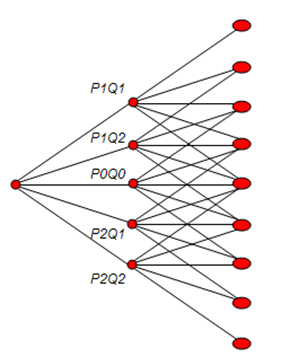
Figure 184.2: Pentanomial lattice (combining two binomial lattices)
Figure 184.3 shows an example Dual Asset Rainbow Option (example file used: Dual-Asset Rainbow Option Pentanomial Lattice). Notice that a high positive correlation will increase both call option and put option values because if both underlying elements move in the same direction, there is a higher overall portfolio volatility. Price and quantity can fluctuate at high-high and low-low levels, generating a higher overall underlying asset value. In contrast, negative correlations will reduce the call and put option values for the opposite reason due to the portfolio diversification effects of negatively correlated variables. Of course, the correlation here is bounded between –1 and +1 inclusive. If a real options problem has more than two underlying assets, use either the SLS or Risk Simulator to simulate the underlying asset’s trajectories and capture their interacting effects in a DCF model. See the varied examples in SLS using pentanomial lattices to solve 3D dual-asset (e.g., spreads, exchange, dual strike, and portfolio) options.
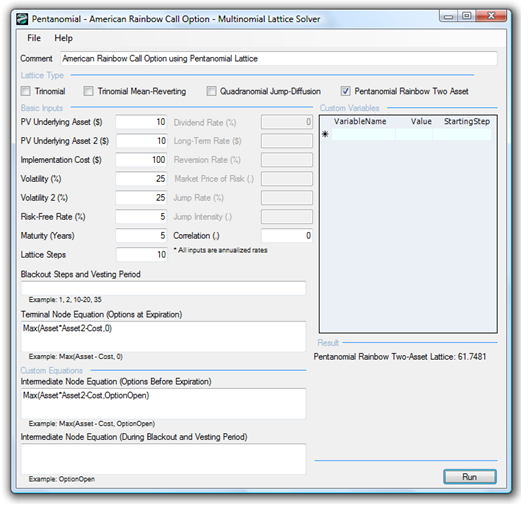
Figure 184.3: Pentanomial lattice solving a dual-asset rainbow option

