File Name: Yield Curve – Vasicek Model
Location: Modeling Toolkit | Yield Curve | Vasicek Model
Brief Description: The Vasicek model is used to create the term structure of interest rates and to reconstruct the yield curve assuming the underlying interest rates are mean reverting and stochastic
Requirements: Modeling Toolkit, Risk Simulator
Modeling Toolkit Function Used: MTVasicekBondYield
This is the Vasicek model used to compute the term structure of interest rates and yield curve. The Vasicek model assumes a mean-reverting stochastic interest rate (Figure 2.35). The rate of reversion and long-run mean rates can be determined using Risk Simulator’s statistical analysis tool. If the long-run rate is higher than the current short rate, the yield curve is upward sloping, and vice versa.
The yield curve is the time-series relationship between interest rates and the time to maturity of the debt. The more formal mathematical description of this relationship is called the term structure of interest rates. As discussed previously, the yield curve can take on various shapes. The normal yield curve means that yields rise as maturity lengthens and the yield curve is positively sloped, reflecting investor expectations for the economy to grow in the future (and, hence, an expectation that inflation rates will rise in the future). An inverted yield curve occurs when the opposite happens, where the long-term yields fall below short-term yields, and long-term investors will settle for lower yields now if they think the economy will slow or even decline in the future, indicative of a worsening economic situation in the future (and, hence, an expectation that inflation will remain low in the future). Another potential situation is a flat yield curve, signaling uncertainty in the economy. The yield curve can also be humped or show a smile or a frown. The yield curve over time can change in shape through a twist or bend, a parallel shift, or a movement on one end versus another.
As the yield curve is related to inflation rates as discussed above, and central banks in most countries have the ability to control monetary policy to target inflation rates, inflation rates are mean reverting in nature. This also implies that interest rates are mean reverting, as well as stochastically changing over time.
A Czech mathematician, Oldrich Vasicek, in a 1977 paper, proved that bond prices on a yield curve over time and various maturities are driven by the short end of the yield curve, or the short-term interest rates, using a risk-neutral martingale measure. In his work, the mean-reverting Ornstein–Uhlenbeck process was assumed; hence the resulting Vasicek model requires that a mean-reverting interest rate process be modeled (rate of mean reversion and long-run mean rates are both inputs in the Vasicek model).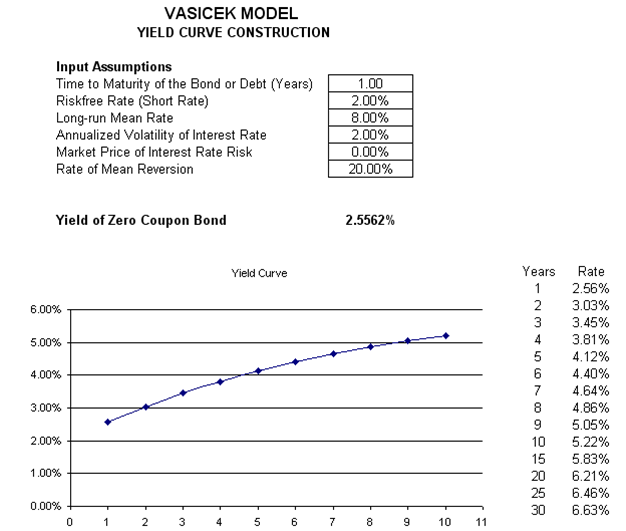
Figure 2.35: Using the Vasicek Model to Generate a Yield Curve

