File Names: Valuation – Warrant – Combined Value; Valuation – Warrant – Put Only; Valuation – Warrant – Warrant Only
Location: Modeling Toolkit | Real Options Models
Brief Description: Frames and values issues of warrants and protective warrants with a put provision
Requirements: Modeling Toolkit, Real Options SLS
This case study provides a sample application of the Real Options SLS software on valuing a warrant (an instrument that can be converted into a stock, similar to a call option) that has a protective put option associated with it. The analysis herein also applies both a customized binomial lattice and a closed-form Black-Scholes model for comparison and benchmarking purposes.
The valuation analysis performed was based on an actual consulting project, but all proprietary information has been modified except for certain basic publicly available information. The accuracy of the results is dependent on this factual information at the time of valuation. This case details the input assumptions used as well as some benchmark due diligence to check the results. Certain technical details have been left out to simplify the case.
The client company very recently acquired a small IT firm. The acquisition consisted of both cash and some warrants, which are convertible into stocks. But because the client’s stocks are fairly volatile, the acquired firm negotiated a protective put to hedge its downside risks. In return for providing this protective put, the client requested that the warrant be exercisable only if the target firm is solvent and its gross margins exceed 33% and are no less than $10 million.
Clearly, this problem cannot be solved using a Black-Scholes model because there exist dividends, a vesting period, a threshold price put protection at which the put can be exercised, and the fact that the put cannot be exercised unless the warrant is converted into a stock but only when the stock price is below $33.
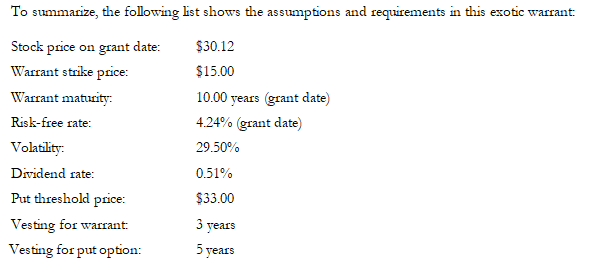
Further, these additional requirements were modeled:
- The protective put option can be exercised only if the warrant is exercised.
- The put option can be exercised only if the stock price is below $33.00 at the time of exercise.
- The warrant can be exercised only if the recipient’s gross margin equals or exceeds 33% and is no less than $10 million. A simulation forecast puts an 85% to 90% uniform probability of occurrence for this event.
- The warrant can be exercised only if the recipient is solvent. Another simulation forecast puts a 90% to 95% uniform probability of occurrence for this event.
- The protective put payout is the maximum spread between the put threshold price less the client’s common stock price or the warrant price.
The risk-free rate is based on the 10-year U.S. Treasury note. The volatility estimate is based on the client’s historical weekly closing prices for the past one, two, and three years. The volatilities are estimated using the standard deviation of the natural logarithmic relative returns, annualized for a year, and then averaged. The dividend rate is assumed to be 0.51% based on available market data on client shares. The total probability of exceeding the gross margin threshold as well as solvency requirements is 80.9375% (calculated using the midpoint probability estimates of both independent events 87.50% times 92.50%, and were the results based on simulation forecasts using historical financial data). The only way to value such a protective put on a warrant is by using binomial lattices. However, a Black-Scholes model is used to benchmark the results.
Warrant Valuation
In order to solve the warrant part of the exotic vehicle, high-level analysis rules need to be created:
- If the period ≥ 3 years, then at maturity, the profit-maximizing decision is:Max (Exercise the warrant accounting for the probability the requirements are met; or let the warrant expire worthless otherwise).
- If the period ≥ 3 years, then prior to maturity, the profit-maximizing decision is:
Max (Exercise the warrant accounting for the probability the requirements are met; or keep the option open for future execution).
- If the period < 3 years, then hold on to the warrant as no execution is allowed.
Protective Put Option Valuation
The same is done for the protective put option:
- If the period ≥ 5 years, then at maturity, the profit-maximizing decision is:Max (If the stock price is < $33, then exercise the warrant and collect the protective put payout, after accounting for the probability the requirements are met; or let the warrant and put option expire worthless).
- If the period ≥ 5 years, then prior to maturity, the profit-maximizing decision is:
Max (If the stock price is < $33, then exercise the warrant and collect the protective put payout, after accounting for the probability the requirements are met; or keep the option open for future execution)
- If the period < 5 years, then hold on to the put option as no execution is allowed.
The binomial model used is a combination of a Bermudan vesting nested option, where all the requirements (vesting periods, threshold price, probability of solvency, probability of exceeding gross margin requirements) have to be met before the warrant can be executed, and the put option that can be executed only if the warrant is executed. However, the warrant can be executed even if the protective put is not executed.
Analytical Results
A summary of results follows. The results start with a decomposition of the Warrant call and the protective put valued independently. These results are then compared to benchmarks to ascertain their accuracy and model reliability. Then a combination of both instruments is valued in a mutually exclusive nested option model. The results of interest are the combined option model, but we can only obtain such a model by first decomposing the parts. The analysis was performed using the SLS software.
To follow along, you can start the Single Asset SLS software and load the relevant example files: Valuation – Warrant – Combined Value; Valuation – Warrant – Put Only; and Valuation – Warrant – Warrant Only.
A. Warrant at Grant Date
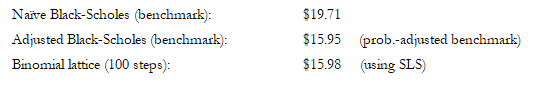
As can be seen, the binomial lattice for the Warrant converges to the Black-Scholes results. The reason for this convergence is that the dividend rate is low, making it not optimal to exercise early, but still worth slightly more than a simple European option. See Figure 198.1 for the details.
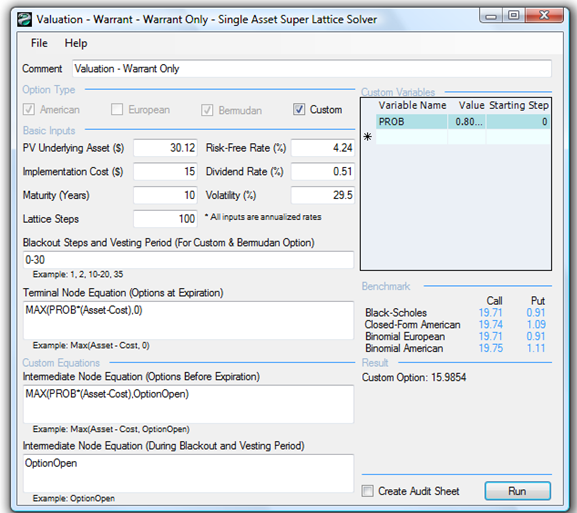
Figure 198.1: Warrant valuation at grant date
B. Protective Put Option at Grant Date
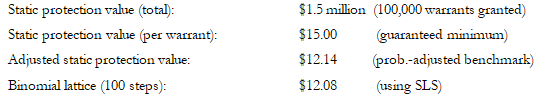
The analysis can be seen in Figure 198.2.
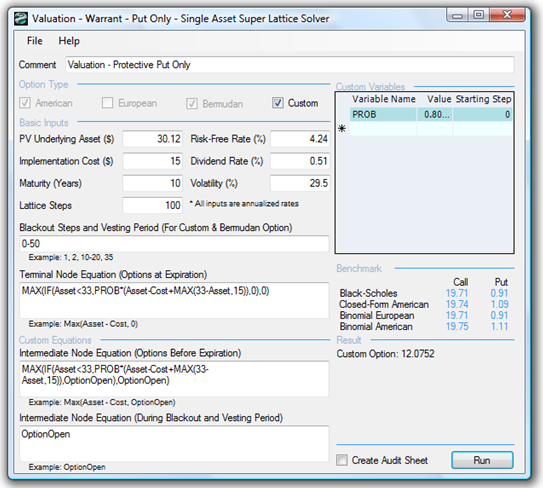
Figure 198.2: Protective put at grant date
The analysis up to this point decomposes the Warrant call and the protective put options, and their values are comparable to the static benchmarks, indicating that the models are specified correctly and the results are accurate. However, the warrant issues cannot be separated from the protective put because they are combined into one instrument. Separating them means that at certain points and conditions in time, the holder can both execute the call and execute the put option protection with another call. This constitutes double-counting. Thus, in such a mutually exclusive condition (either a call is executed or a protective put is executed with the call, not both), a combination valuation is performed. The results are shown next.
C. Combination of Warrant and Protective Put Option at Grant Date
Figure 198.3 illustrates the analysis performed.
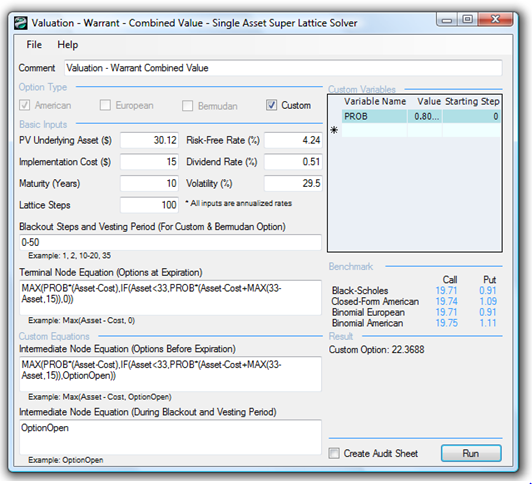
Figure 198.3: Combined Warrant with protective put at grant date
Using Black-Scholes call and put option models as benchmarks, we see that the sought-after result of $22.37 is valid, after considering that the decompositions of the model are also valid. Clearly, the total combined value has to exceed the Black-Scholes as the Warrant-put is an American option (with vesting requirements). To summarize, the analysis cannot be completed without the use of the Single Asset SLS software. Even when solving such complicated instruments, using the software makes pricing relatively straightforward.

