As mentioned, correlation does not imply causality, but causality usually implies correlation. However, correlation can come in many flavors, starting with the basics like linear and nonlinear correlation, where we quantitatively compute the pairwise co-movement relationship among two variables. Correlations of the variable to itself in the past is also an important characteristic. This autocorrelation implies that the past is a good predictor of the future. The following are some correlation-related quantitative methods.
- Autocorrelation and Partial Autocorrelation. One very simple approach to test for autocorrelation is to graph the time series of a regression equation’s residuals. If these residuals exhibit some cyclicality, then autocorrelation exists. Another more robust approach to detect autocorrelation is the use of the Durbin–Watson statistic, which estimates the potential for a first-order autocorrelation. The Durbin–Watson test employed also identifies model misspecification, that is, if a time-series variable is correlated to itself one period prior. Many time-series data tend to be autocorrelated to their historical occurrences. Autocorrelation is applicable only to time-series data. This relationship can exist for multiple reasons, including the variables’ spatial relationships (similar time and space), prolonged economic shocks and events, psychological inertia, smoothing, seasonal adjustments of the data, and so forth.
- Autocorrelation Durbin–Watson AR(1) Test. The Durbin–Watson test can be used to determine the autocorrelation of one lag period or AR(1) process. Typically, the one-period lag is the most predominant effect, as the further one travels in time, the lower the potential impact or correlation to the future value.
- Control Charts: C, NP, P, R, U, X, XMR. Control charts are not used to determine cross-correlations of one variable against another, but a potential relationship with itself and to see if the variable remains under statistical limits or statistical control. Sometimes specification limits of a process are not set; instead, statistical control limits are computed based on the actual data collected (e.g., the number of defects in a manufacturing line). The upper control limit (UCL) and lower control limit (LCL) are computed, as are the central line (CL) and other sigma levels. The resulting chart is called a control chart, and if the process is out of control, the actual defect line will be outside of the UCL and LCL lines for a certain number of times.
- Correlation Matrix (Linear and Nonlinear). The Pearson’s linear product-moment correlation (commonly referred to as the Pearson’s R), as well as the nonlinear Spearman rank-based correlation between variable pairs, can be computed as a correlation matrix. The correlation coefficient ranges between –1.0 and +1.0, inclusive. The sign indicates the direction of association between the variables, while the coefficient indicates the magnitude or strength of association.
- Covariance Matrix. The variance-covariance matrix for a sample and population as well as a Pearson’s linear correlation matrix can be computed. However, covariance matrices are more difficult to interpret because, theoretically, the values of covariances are between negative and positive infinity. When you take the covariance (cov) and standardize them using the two variables’ standard deviations (σ), you obtain the correlation coefficient ρ, which is a lot simpler to interpret as the values always fall between –1.0 and +1.0, inclusive. In other words,
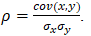
- Factor Analysis. Factor Analysis is used to analyze interrelationships within large numbers of variables and simplifying said factors into a smaller number of common factors. The method condenses information contained in the original set of variables into a smaller set of implicit factor variables with minimal loss of information. The analysis is related to the Principal Component Analysis(PCA) by using the correlation matrix and applying PCA coupled with a Varimax matrix rotation to simplify the factors.
- Kendall’s Tau Correlation. Kendall’s Tau is a nonparametric correlation coefficient, considering concordance or discordance, based on all possible pairwise combinations of ordinal ranked data variables. The null hypothesis tested is that there is zero correlation between the two variables. The method can be applied to values with ties (identical and repeated values) or without considering ties.
- Partial Correlations (Using Correlation Matrix). The Partial Correlation Matrix can be computed using an existing N × N full correlation matrix. The partial correlation measures the degree of association, just like a regular correlation coefficient, between two random variables, but with the effects of a set of controlling random variables removed or blocked. Using a simple correlation coefficient may provide misleading results if there are other confounding variables that are related to the two variables of interest.
- Principal Component Analysis. Principal component analysis, or PCA, makes multivariate data easier to model and summarize. To understand PCA, suppose we start with N variables that are unlikely to be independent of one another, such that changing the value of one variable will change another variable. PCA modeling will replace the original N variables with a new set of M variables that are less than N but are uncorrelated to one another, while at the same time, each of these M variables is a linear combination of the original N variables so that most of the variation can be accounted for just using fewer explanatory variables.

