File Name: Real Options – Jump-Diffusion Calls and Puts Using Quadranomial Lattices
Location: Modeling Toolkit | Real Options Models
Brief Description: Computes the options where the underlying asset follows a jump-diffusion process (e.g., oil and electricity prices), using quadranomial lattices
Requirements: Modeling Toolkit, Real Options SLS
The Jump-Diffusion Calls and Puts model for both American and European options applies the Quadranomial Lattice approach. This model is appropriate when the underlying variable in the option follows a jump-diffusion stochastic process. Figure 187.1 illustrates an underlying asset modeled using a jump-diffusion process. Jumps are commonplace in certain business variables such as the price of oil and the price of gas where prices take sudden and unexpected jumps (e.g., during a war). The underlying variable’s frequency of jump is denoted as its Jump Rate, and the magnitude of each jump is its Jump Intensity.
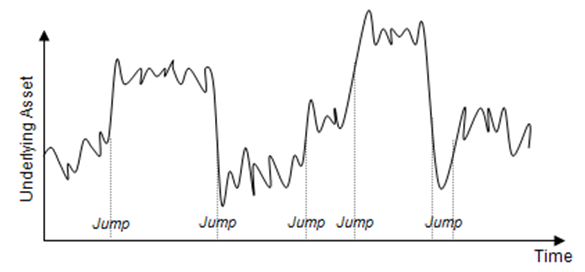 Figure 187.1: Jump-diffusion process
Figure 187.1: Jump-diffusion process
The binomial lattice is able to capture only a stochastic process without jumps (e.g., Brownian Motion and Random Walk processes). When there is a probability of jump (albeit a small probability that follows a Poisson distribution), additional branches are required. The quadranomial lattice (four branches on each node) is used to capture these jumps, as seen in Figure 187.2.
Be aware that due to the complexity of the models, some calculations with higher lattice steps may take slightly longer to compute. Furthermore, certain combinations of inputs may yield negative implied risk-neutral probabilities and result in a noncomputable lattice. In that case, make sure the inputs are correct (e.g., Jump Intensity has to exceed 1, where 1 implies no jumps; check for erroneous combinations of Jump Rates, Jump Sizes, and Lattice Steps). The probability of a jump can be computed as the product of the Jump Rate and time-step δt. Figure 187.3 illustrates a sample Quadranomial Jump-Diffusion Option analysis (example file used: Jump Diffusion Calls and Puts Using Quadranomial Lattices). Notice that the Jump-Diffusion call and put options are worth more than regular calls and puts. This is because, with the positive jumps (10% probability per year with an average jump size of 1.50 times the previous values) of the underlying asset, the movements of the asset are more significant than without any jumps. This results in the call and put options being worth more, even with the same volatility (i.e., $34.69 compared to $31.99 and $15.54 compared to $13.14).
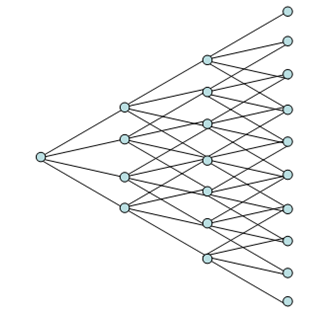
Figure 187.2: Quadranomial lattice
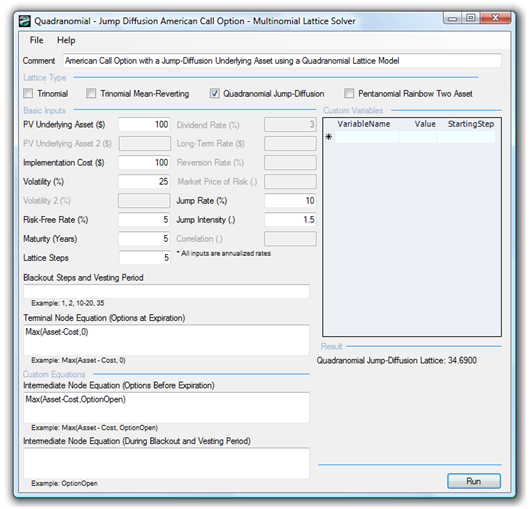
Figure 187.3: Quadranomial lattice results on jump-diffusion options

