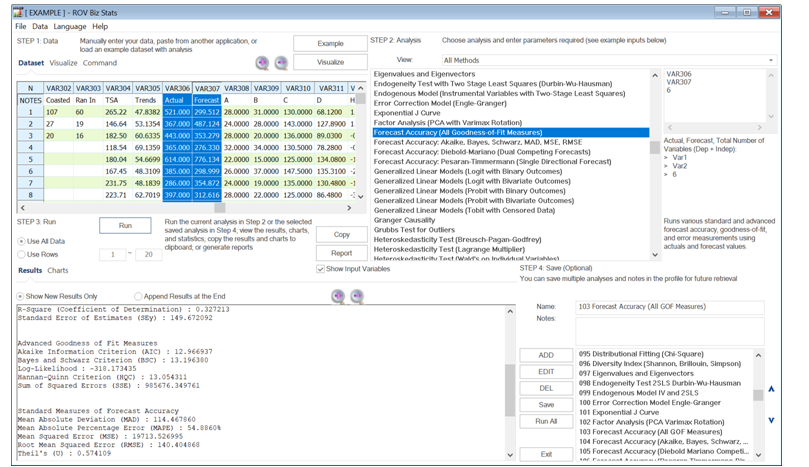
A statistically significant and internally valid model may or may not have practical significance. This is where external validity comes in. While internal validity looks at the individual constructs of the model, external validity looks at the entire model and measures how much that model may explain the predicted variable. Typically, external validity is measured using a variety of error formulae. The typical measure is the R-square and adjusted R-square (the coefficient of determination and adjusted coefficient of determination). The R-square is simply the linear correlation (R) between the actual and predicted values, squared. While R has a domain between –1.00 and +1.00, its squared value will always lie between 0.00 and 1.00. Hence, the R-square is a percentage measure, which shows how much of the variation of the dependent variable can be explained simultaneously by all of the independent variables in the model. The higher the R-square, the higher the external validity of the model. However, in multivariate models, adding additional exogenous variables that may or may not be internally valid will usually increase the R-square value. This is where the adjusted R-square comes in. The adjusted R-square will adjust for the added independent variables and penalizes the R-square for having too many independent variables that do not statistically significantly increase the R-square sufficiently. This means that with added extraneous variables, the adjusted R-square may actually decline, making it a more conservative and better estimate of a model’s external validity.
In addition, along the lines of penalizing added variables, where holding everything else constant, if the predictive powers of two models are identical but one uses fewer predictor variables, then the more parsimonious model wins out. Based on the theory of parsimony and penalization of too many extraneous variables, other measures of external validity were created, such as the Akaike Information Criterion or the Bayes–Schwarz Criterion. These are relative measures of external model errors and are typically used to compare different model specifications to identify the lower error scores. The following are additional external validity error measures. Those denoted with an asterisk * are values that we would rather see an increase, versus the remaining error measures where the lower the error, the higher the external validity of the model.
*R-Squared
*Adjusted R-Squared
*Maximum Likelihood
Akaike Information Criterion (AIC)
Bayes and Schwarz Criterion (BSC)
Hannan–Quinn Criterion (HQC)
Mean Absolute Deviation (MAD)
Mean Absolute Percentage Error (MAPE)
Mean Squared Error (MSE)
Median Absolute Error (MdAE)
Median Absolute Percentage Error (MdAPE)
Root Mean Square Log Error (RMSLE)
Root Mean Square Percentage Error Loss (RMSPE)
Root Mean Squared Error (RMSE)
Root Median Square Percentage Error Loss (RMdSPE)
Sum of Squared Errors (SSE)
Symmetrical Mean Absolute Percentage Error (sMAPE)
Theil’s U1 Accuracy (U1)
Theil’s U2 Quality (U2)