File Name: Real Options – Multiple Assets Competing Options (3D Binomial)
Location: Modeling Toolkit | Real Options Models
Brief Description: Computes a 3D binomial option where there are multiple underlying assets and the option holder has the ability to purchase the asset with the highest value
Requirements: Modeling Toolkit, Real Options SLS
This model illustrates the power of real options analysis and the ability of the Real Options SLS software to solve customizable options. This two-underlying-assets model is sometimes called a 3D binomial model, as there are multiple assets (Figure 189.1). The problem is solved using the multiple assets and multiple phased MNLS module in the SLS software. The critical pieces are the terminal and intermediate equations. In this example, we solve a call option on the maximum (i.e., given that there are multiple underlying assets, this option allows the holder to execute and purchase the asset that is the highest when executed). The option can be an American, Bermudan, or European option.
To create an American option, use:
Terminal equation: Max(FirstAsset-Cost,SecondAsset-Cost,0)
Intermediate equation: Max(FirstAsset-Cost,SecondAsset-Cost,OptionOpen)
To create a Bermudan option, simply add in the Blackout and Vesting Period Steps to cover the appropriate time periods in the lattice when the option cannot be executed. For instance, for a five-year project solved using a 100-step lattice, if the blackout or vesting period is the first three years (option cannot be executed in Years 0 to 3, including the current time zero), then set the blackout steps to be 0–60, and make sure you type in OptionOpen for the blackout equation. To create a European option, keep the same terminal equation but change the intermediate equation to OptionOpen.
Note that 3D options can also be solved using pentanomial lattices in SLS.
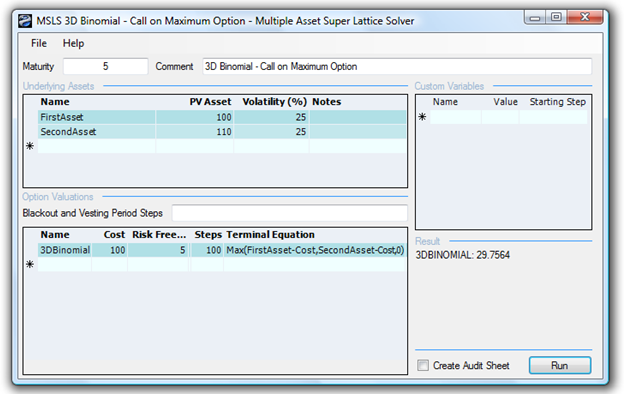
Figure 189.1: Multiple assets competing option

