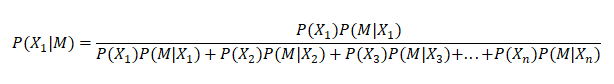The material below comprises excerpts from books by Dr. Johnathan Mun, our CEO and founder, such as Readings in Certified Quantitative Risk Management, 3rd Edition, and Quantitative Research Methods Using Risk Simulator and ROV BizStats Software Applying Econometrics, Multivariate Regression, Parametric and Nonparametric Hypothesis Testing, Monte Carlo Risk Simulation, Predictive Modeling, and Optimization, 4th Edition (https://www.amazon.com/author/johnathanmun). All screenshots and analytical models are run using the ROV Risk Simulator and ROV BizStats software applications. Statistical results shown are computed using Risk Simulator or BizStats. Online Training Videos are also available on these topics as well as the Certified in Quantitative Risk Management (CQRM) certification program. All materials are copyrighted as well as patent protected under international law, with all rights reserved.
Bayes’ Theorem is a mathematical formula that deals with conditional probabilities. That is, it provides a means for updating probabilities based on relevant evidence that has occurred. Also, the theorem is useful when trying to solve a probability problem that seems intractable if not unsolvable at first pass. For example, suppose you find yourself standing outside of three darkened rooms labeled A, B, and C, and you know that in each room there are two people, either male (MM), female (FF), or one of each (MF). Therefore, P(M|A)=1.0; P(M|B)=0.5 and P(M|C)=0. See the following diagram:
 You take a flashlight and enter a room at random where you first shine the light on a male. What is the probability that you have entered room A? In other words, find P(A|M).
You take a flashlight and enter a room at random where you first shine the light on a male. What is the probability that you have entered room A? In other words, find P(A|M).
Seeing that we know the probability rule where P(M and A)=P(M∩A)=P(M)P(A│M), solving for P(A│M), we get
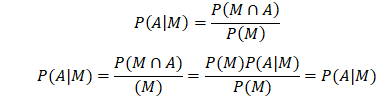
but here, we are stuck in a circular loop! We need to use Bayes’ Theorem to solve the problem:
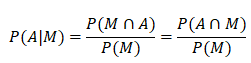
since commutability holds where ![]() Hence, from here,
Hence, from here,
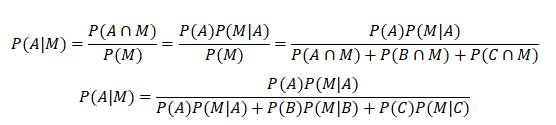
represents the Bayes’ Theorem. So,
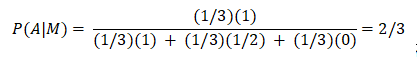
Bayes’ Theorem can be generalized to: