File Name: Options Analysis – Options on Debt
Location: Modeling Toolkit | Options Analysis | Options on Debt
Brief Description: Computes options using the binomial lattice approach, assuming that the yield curve and the term structure of interest rates change over time (both interest rates and volatility of interest rates are changing over time)
Requirements: Modeling Toolkit
Modeling Toolkit Functions Used: MTBDTInterestRateLattice, MTBDTZeroPriceLattice, MTBDTAmericanCallonDebtLattice, MTBDTAmericanPutonDebtLattice, MTBDTEuropeanCallonDebtLattice, MTBDTEuropeanPutonDebtLattice, MTBDTAmericanCallonDebtValue, MTBDTAmericanPutonDebtValue, MTBDTEuropeanCallonDebtValue, MTBDTEuropeanPutonDebtValue
This model is used to compute the American and European options on debt using a binomial lattice modified to account for changing volatilities and the term structure of interest rates over the life of the option (Figure 109.1). It provides a sample template for building interest rate pricing lattices using the Modeling Toolkit functions and is set up to only compute up to 10 steps. Using this template, you can generate additional steps as required, as well as create customized lattices to value any types of embedded-option debt instruments. Also, you can use the Real Options SLS software to value many types of options and options-embedded instruments.
The modified lattices introduced in the preceding few chapters are specific to financial instruments that depend on interest rates, where the underlying asset’s fundamental values are driven by interest rate fluctuations. Please see those chapters for instructions on setting up these lattice matrices and how to calibrate these matrices for the term structure of interest rates and their localized interest rate volatilities. The present model also shows how to compute the American and European call and put options on the bond. Note that entire lattices can be built using the “lattice” functions, or the value of the bond option can be computed simply by using the “value” functions in the model.
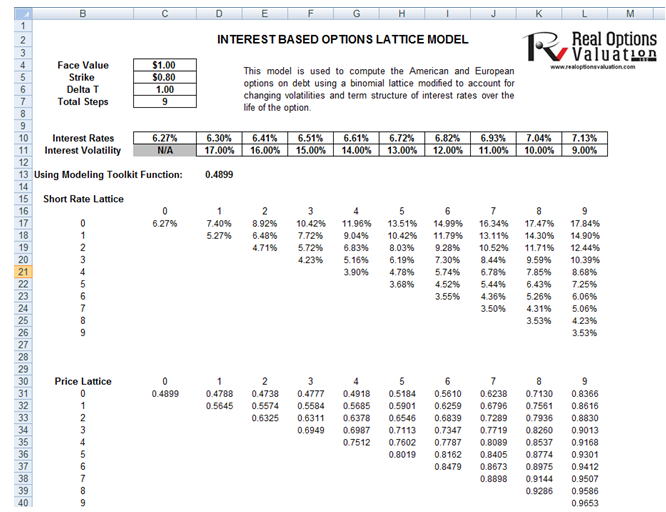
Figure 109.1: Generating binomial lattices on debt options

