Principal Component Analysis (PCA) is a way of identifying patterns in data, and recasting the data in such a way as to highlight their similarities and differences. Patterns of data are very difficult to find in high dimensions when multiple variables exist, and higher dimensional graphs are very difficult to represent and interpret. Once the patterns in the data are found, they can be compressed, and the number of dimensions is now reduced. This reduction of data dimensions does not mean much reduction in loss of information. Instead, similar levels of information can now be obtained by a fewer number of variables.
PCA is a statistical method that is used to reduce data dimensionality using covariance analysis among independent variables by applying an orthogonal transformation to convert a set of correlated variables data into a new set of values of linearly uncorrelated variables named principal components. The number of computed principal components will be less than or equal to the number of original variables. This statistical transformation is set up such that the first principal component has the largest possible variance accounting for as much of the variability in the data as possible, and each subsequent component has the highest variance possible under the constraint that it is orthogonal to or uncorrelated with the preceding components. Thus, PCA reveals the internal structure of the data in a way that best explains the variance in the data. Such dimensionality reduction is useful to process high-dimensional datasets while still retaining as much of the variance in the dataset as possible. PCA essentially rotates the set of points around their mean in order to align with the principal components. Therefore, PCA creates variables that are linear combinations of the original variables. The new variables have the property that the variables are all orthogonal. Factor analysis is similar to PCA, in that factor analysis also involves linear combinations of variables using correlations whereas PCA uses covariance to determine eigenvectors and eigenvalues relevant to the data using a covariance matrix. Eigenvectors can be thought of as preferential directions of a dataset or main patterns in the data. Eigenvalues can be thought of as quantitative assessments of how much a component represents the data. The higher the eigenvalues of a component, the more representative it is of the data.
As an example, PCA is useful when running multiple regression or basic econometrics when the number of independent variables is large or when there is significant multicollinearity in the independent variables. PCA can be run on the independent variables to reduce the number of variables and to eliminate any linear correlations among the independent variables. The extracted revised data obtained after running PCA can be used to rerun the linear multiple regression or linear basic econometric analysis. The resulting model will usually have slightly lower R-squared values but potentially higher statistical significance (lower p-value). Users can decide to use as many principal components as required based on the cumulative variance.
Principal Component Analysis is related to another method called Factor Analysis. Principal component analysis makes multivariate data easier to model and summarize. Figure 15.27 illustrates an example where we start with 9 independent variables that are unlikely to be independent of one another, such that changing the value of one variable will change another variable. Recall that this multicollinearity effect can cause biases in a multiple regression model. Both principal component and factor analysis can help identify and eventually replace the original independent variables with a new set of smaller variables that are less than the original but are uncorrelated to one another, while, at the same time, each of these new variables is a linear combination of the original variables. This means most of the variation can be accounted for by using fewer explanatory variables. Similarly, factor analysis is used to analyze interrelationships within large numbers of variables and simplifying said factors into a smaller number of common factors. The method condenses information contained in the original set of variables into a smaller set of implicit factor variables with minimal loss of information. The analysis is related to the principal component analysis by using the correlation matrix and applying principal component analysis coupled with a varimax matrix rotation to simplify the factors.
In Figure 15.27, we start with 9 independent variables, which means the factor analysis or principal component analysis results will return a 9 × 9 matrix of eigenvectors, and 9 eigenvalues. Typically, we are only interested in components with eigenvalues > 1. Hence, in the results, we are only interested in the first three or four factors or components (some researchers would plot these eigenvalues and call it a scree plot, which can be useful for identifying where the kinks are in the eigenvalues). Notice that the fourth factor (the fourth column in the figure) returns a cumulative proportion of 72.31%. This means that using these four factors will explain approximately three-quarters of the variation in all the independent factors themselves. Next, we look at the absolute values of the eigenvalue matrix. It seems that variables 2, 3, 7, and 8 can be combined into a new variable in factor 1, variables 1 and 9 as the second factor, variable 6 by itself as the third factor, and variable 4 by itself as a new variable. This can be done separately and outside of principal component analysis.
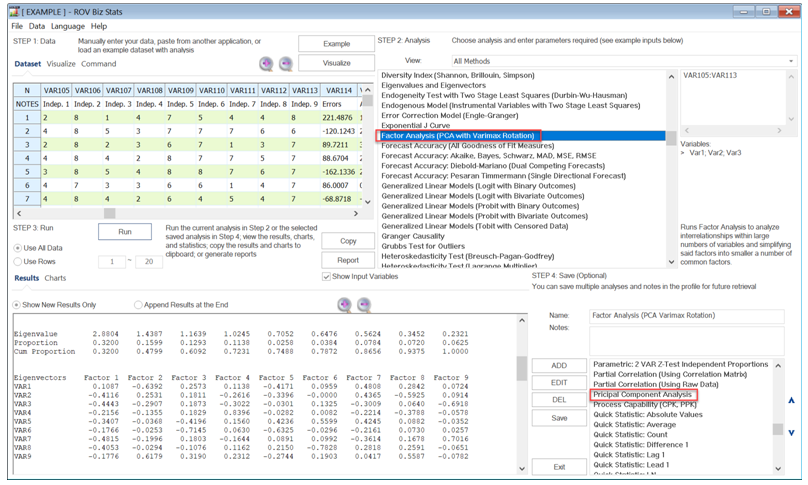
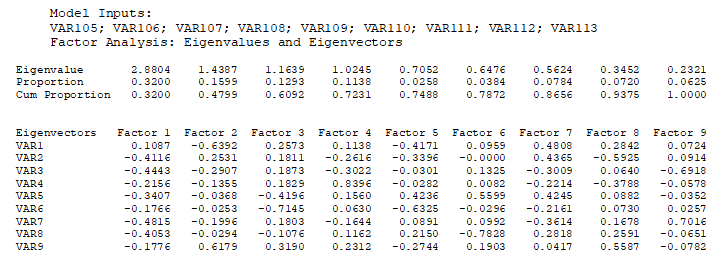
Figure 15.27: Principal Component Analysis

