Figure 6.1 illustrates the complex interrelationships among the various distributions described above. Some distributions are simply special cases of other distributions (e.g., standard-normal distribution is a special case of the normal distribution), limiting cases (e.g., the t-distribution approaches the normal distribution at the limit), modifications of others (e.g., power 3 is a modification of the power distribution by adding a location and multiplicative factor parameter), and mathematical transformations (e.g., log gamma is a logarithmic transformation of the gamma distribution). In other cases, some distributions can be obtained through a mathematical convolution of multiple identical distributions (e.g., the sum of uniform distributions converges to the normal distribution) or different distributions (e.g., the division of two different chi-square distributions approaches the F-distribution). Therefore, newer, and more complex distributions can be developed using these basic building blocks. However, it is mathematically complex to create or model new distributions analytically, but, by using Monte Carlo risk simulation methods, new and unique distributions can be readily and easily created by simply adding, subtracting, multiplying, dividing, and applying any other combinations of mathematical operators among multiple simulation assumptions to generate your own unique probability distribution, without the need for complex mathematics.
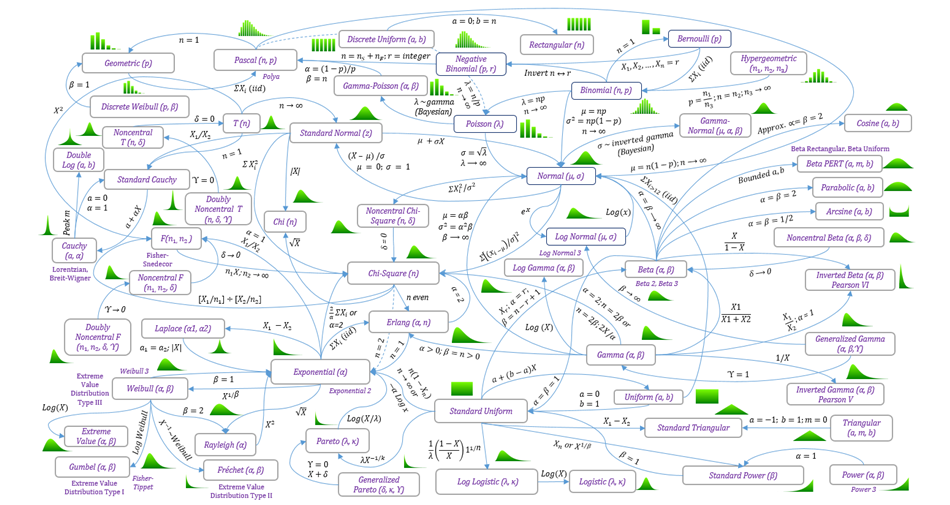
Figure 6.1: Relationships Among Probability Distributions

