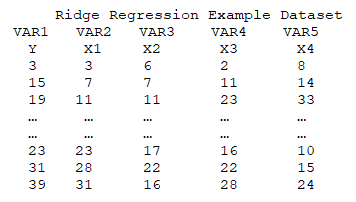A Ridge regression comes with a higher bias than an Ordinary Least Squares (OLS) multiple regression but has less variance. It is more suitable in situations with high Variance Inflation Factors (VIF) and multicollinearity or when there is a high number of variables compared to data points. In a standard multiple regression model, we minimize the fitted sum of squared errors where ![]() but in a high VIF dataset with near perfect collinearity, the matrix is not invertible and cannot be solved. In this situation, the sum of squares is penalized with an added term where
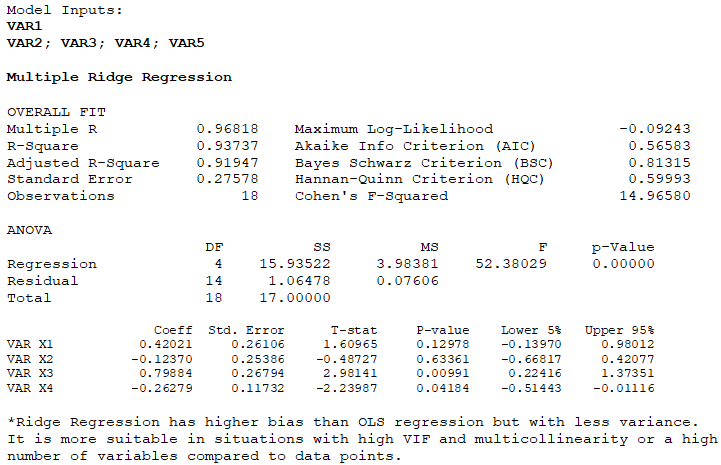
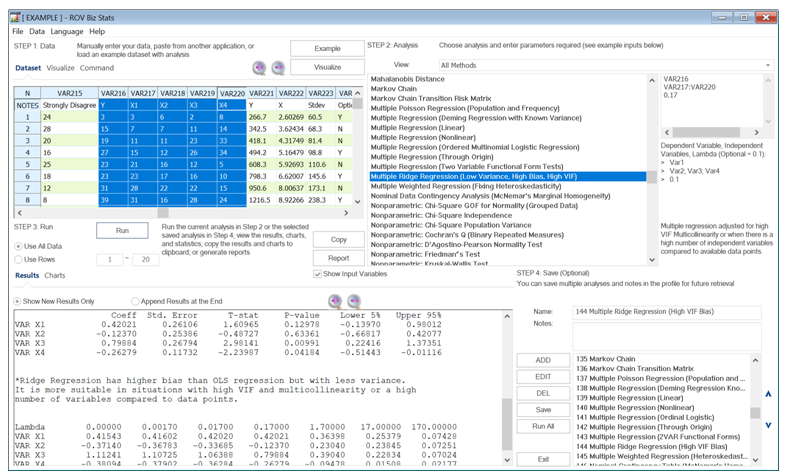
but in a high VIF dataset with near perfect collinearity, the matrix is not invertible and cannot be solved. In this situation, the sum of squares is penalized with an added term where![]() and λ is considered the adjustment parameter. When λ=0, the results revert to an OLS approach. A small λ generates estimates with less bias but with a higher variance, versus a large λ that generates higher bias with less variance. The idea is to select a value that balances bias and variance, which might require trial and error. Finally, ridge-based regressions are suitable only when there is high VIF or significant multicollinearity. As discussed, multicollinearity can be solved by simply removing the offending independent variable(s) and running a standard regression. A sample dataset and results from BizStats are shown below.
and λ is considered the adjustment parameter. When λ=0, the results revert to an OLS approach. A small λ generates estimates with less bias but with a higher variance, versus a large λ that generates higher bias with less variance. The idea is to select a value that balances bias and variance, which might require trial and error. Finally, ridge-based regressions are suitable only when there is high VIF or significant multicollinearity. As discussed, multicollinearity can be solved by simply removing the offending independent variable(s) and running a standard regression. A sample dataset and results from BizStats are shown below.