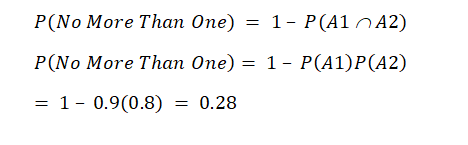The Poisson distribution describes the number of times an event occurs in a given interval, such as the number of telephone calls per minute or the number of errors per page in a document.
The three conditions underlying the Poisson distribution are:
- The number of possible occurrences in any interval is unlimited
- The occurrences are independent. The number of occurrences in one interval does not affect the number of occurrences in other intervals.
- The average number of occurrences must remain the same from interval to interval.
The mathematical constructs for the Poisson are as follows:
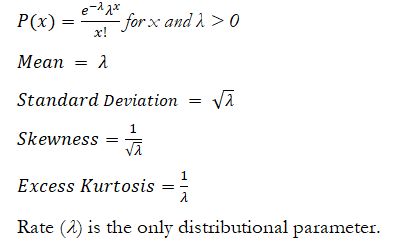
Input requirements: Rate > 0 and ≤ 1000 (that is, 0.0001 ≤ Rate ≤ 1000)
To reiterate, the following are the main characteristics of Poisson:
- Assumes indistinct trials.
- Models rare events where the typical probability of occurrences small.
- When N ≥ 20 and μ = np is ≤ 7, a Poisson is a good fit.
- Statistical independence is assumed between trials and events.
- Interval should be subdivided into subintervals such as time and space (area).
- Assumes the probability of two or more occurrences in the same subinterval is zero.
- A good hint on when to use a Poisson distribution is when events based on time or area are measured as well as for events occurring on average.
Example: A tire service center has the capacity of servicing 6 customers in an hour. From prior experience, on average, 3 an hour shows up. The owner is afraid that there might be insufficient manpower to handle the overcrowding of more than 6 customers. What is the probability that there will be exactly 6 customers? What about over 6 customers?
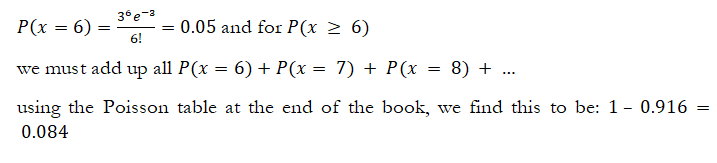
Examples: Hypergeometric and Poisson
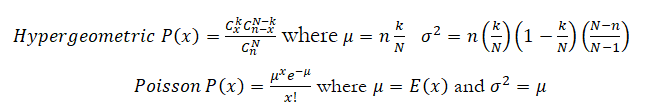
Example 1: See if you can tell which discrete distribution(s) best describes the following conditions and why (i.e., if the problem could be solved using a binomial, hypergeometric, or Poisson distribution):
- A firm owns 25 trucks, and each truck has a probability of 0.01 of breaking down. What is the probability of exactly 2 trucks breaking down in any given hour?
POISSON, as no distinct trials, hours could be broken up into subintervals of space and time. - A fighter aircraft in combat has a probability of 0.01 of being shot down. What is the probability of an aircraft being shot down at least once in 15 missions?
BINOMIAL, as distinct trials and distinct success and failures, as well as statistical independence between trials. - Four out of five dentists prefer Coolpaste to other leading brands of toothpaste. Out of 50 dentists in the local area, if you randomly select 20 of them, what is the probability that 15 of them will prefer Coolpaste?
HYPERGEOMETRIC, as given combinations of things and given sample and population parameters, as well as sampling without replacement is assumed. - If on average you find a mistake on 8 square yards of a rug, what is the probability that there will be a mistake on 70 yards of rug?
POISSON, as using indistinct trials, length could be broken up into an infinite number of subintervals. - Aunt Matilda’s world-famous fruitcake contains on average 20 nuts per slice. If 20 mathematicians arrive and share the cake, what is the probability that each will get at least 12 nuts? What if an additional 45 Hell’s Angels bikers crash the party and she will have to divide the cake for everyone?
POISSON, as using indistinct trials, the area could be broken up into an infinite number of subintervals (slices).
Example 2: Calculate the respective probability for scenarios i, ii, and iii above.
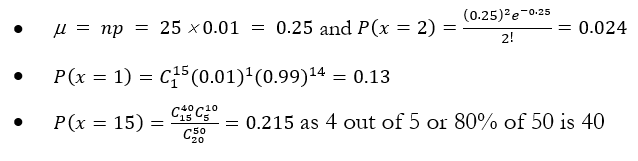
Exercises: Discrete Probability Distributions
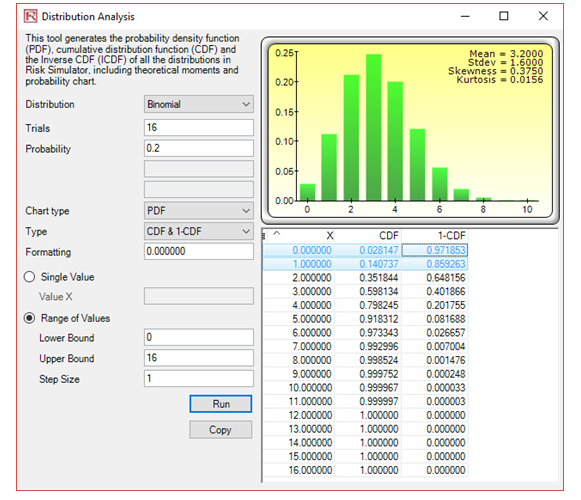
1. A new office complex consists of 16 office suites, each of which is rented on a lease. There is a 20% chance that any single-office suite will be vacated before the lease is up.
a. What discrete probability distribution should you be using and why?
Binomial, as there are 2 outcomes, finite trials, fixed probabilities, discrete events, and independence.
b. What is the probability that at least one suite will be vacated before the lease expires?
We require P(at least one vacated) = P(x = 1) + P(x = 2) + … + P(x = 16), which is the same as P(at least one vacated) = 1 – P(x = 0) since they are complementary:
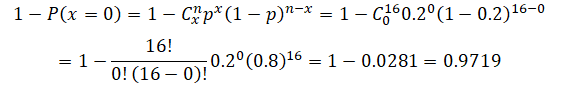
c. What is the probability that no more than one suite will be vacated?
P(No more than one) = P(x = 0) + P(x = 1) and using the binomial, we have
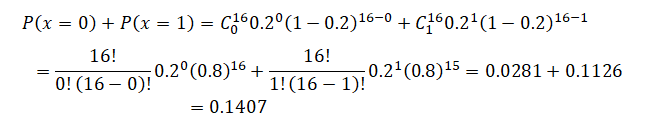
2. In a 2021 article, Consumer Reports found widespread contamination and mislabeling of seafood in New York supermarkets. The study revealed that 40% of the swordfish pieces available for sale had levels of mercury above the Food and Drug Administration maximum amounts. In a random sample of 5 swordfish pieces, find the following probabilities:
a. Four have mercury levels above the maximum levels
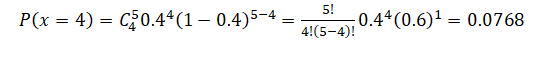b. Two have mercury levels above the maximum levels
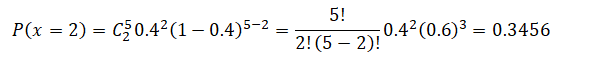
c. Which discrete probability distribution should you be using and why?
Binomial, since there are two outcomes, finite trials, discrete, fixed probabilities, and independence between trials.
3. A commercial for Tasteless sugarless chewing gum claims that 3 out of 4 dentists who recommend sugarless gum to their patients recommend Tasteless. Suppose this claim was established following a survey of 4 dentists randomly selected from a group of 20 dentists. What is the probability that at least 3 of the 4 dentists would recommend Tasteless if, in fact, only 50% of the original group of 20 dentists favor that brand? What discrete distribution should you use?
P (at least 3) = P(3) + P(4) using the hypergeometric distribution since sampling without replacement, which creates dependence. We thus have:
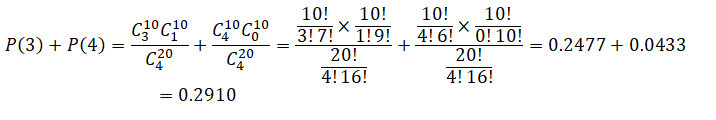
4. The Labor Management Reporting and Disclosure Act of 1959 prescribes fiduciary responsibilities for union officials and makes embezzlement of union funds a crime. In the 38 years since the act was passed, civil suits have been filed under the law randomly and independently of one another at an average rate of 2.7 suits per month.
a. What is the probability that NO suits are filed in a given month?
Follows a Poisson distribution where
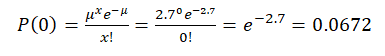b. What is the probability of no more than 2 suits being filed?
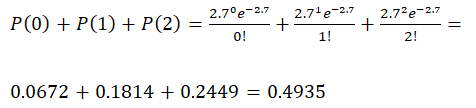
5. Calculate the following:
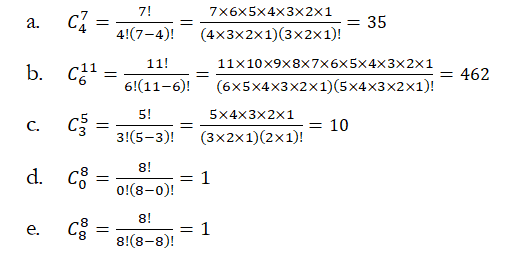
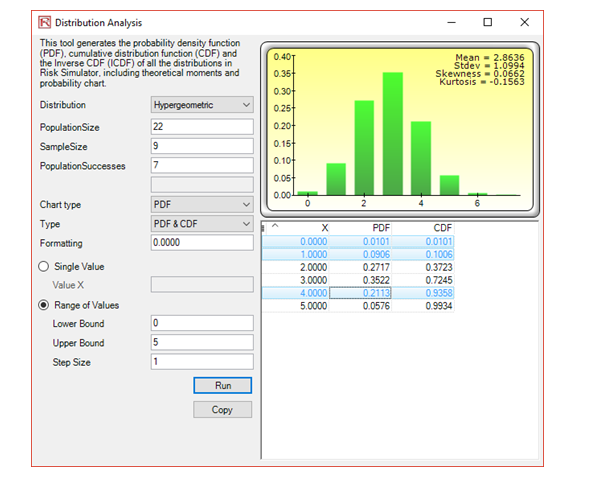
6. Suppose there are 420 applicants for 7 positions at a certain company, and the company is able to narrow the field to 22 equally qualified applicant finalists. Of the finalists, 9 are minority candidates. Assume that the 7 who are chosen are selected at random from this final group of 22. Calculate the probability that:
a. 4 of the 7 hired are minority candidates
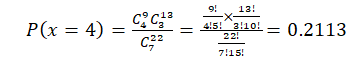
b. None of the minority candidates is hired
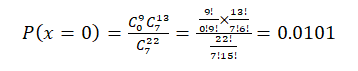c. Only 1 of those hired is a minority candidate
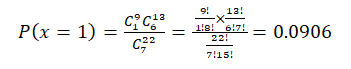d. Which discrete distribution should be used here?
Hypergeometric (selection without replacement and dependence)
7. A sprinkler system inside an office building has two types of activation devices, A1 and A2, which operate independently. In case of fire, the probability that device A1 operates correctly is 90% and 80% that device A2 operates correctly. If a fire breaks out, find the probability that:
a. Both devices operate correctly.
b. At least one device operates correctly.
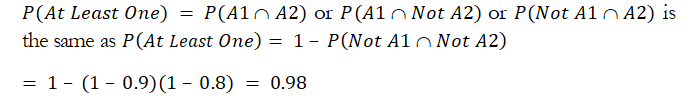
c. Exactly one device fails to operate correctly.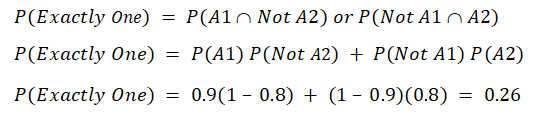
d. Neither device operates correctly.
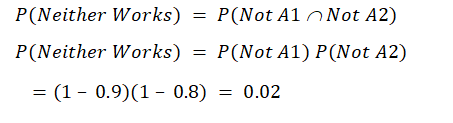e. No more than one device operates correctly.
