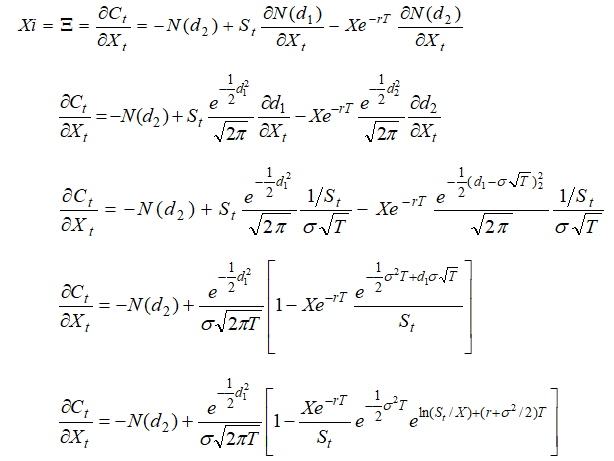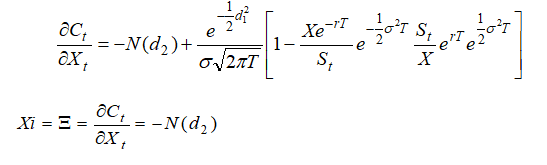File Name: Sensitivity – Greeks
Location: Modeling Toolkit | Sensitivity | Greeks
Brief Description: Computes an option’s instantaneous sensitivity parameters or Greeks
Requirements: Modeling Toolkit, Risk Simulator
Modeling Toolkit Functions Used: MTCallDelta, MTCallGamma, MTCallTheta, MTCallRho, MTCallVega, MTPutDelta, MTPutGamma, MTPutTheta, MTPutRho, MTPutVega
This model illustrates the option’s Greeks to determine the instantaneous sensitivities to each of the inputs (Figure 129.1). Be careful as these values are based on partial differential equations for instantaneous changes and may not represent the changes of, say, some percentage differential. To determine the sensitivities of each input by varying one input at a time, use Risk Simulator’s Tornado tool or see the Sensitivity –Tornado and Sensitivity Nonlinear model instead. Greeks are sometimes useful for setting up the delta and delta-gamma hedges, to completely reduce the risk in a portfolio of options and underlying assets.
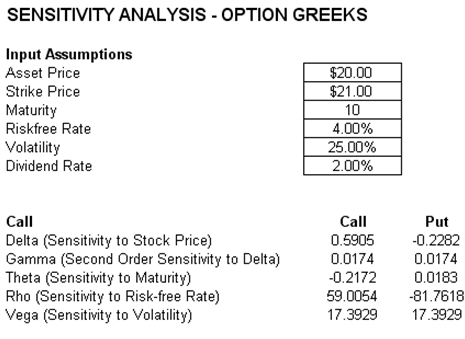
Figure 129.1: Option’s Greeks
Using the corollary outputs generated by options theory, we can obtain the Greeks––namely, Delta, Gamma, Rho, Theta, Vega, and Xi––as a form of sensitivity analysis. By definition, sensitivity analysis, or stress testing, looks at the outcome of the change in the option price given a change in one unit of the underlying variables. In our case, these sensitivities reflect the instantaneous changes of the value of the option given a unit change in a particular variable, ceteris paribus. In other words, we can form a sensitivity table by simply looking at the corresponding values in Delta, Gamma, Rho, Theta, Vega, and Xi. Delta provides the change in the value of the option given a unit change in the present value of the underlying asset’s cash flow series. Gamma provides the rate of change in delta given a unit change in the underlying asset’s cash flow series. Rho provides us with the change in the value of the option given that we change the interest rate one unit; Theta looks at the change per unit of time; Vega looks at the change per unit of volatility; and Xi looks at the change per unit of cost. In other words, one can provide a fairly comprehensive view of the way the value of the option changes given changes in these variables, thereby providing a test of the sensitivity of the option’s value. A worst-case, nominal case, and best-case scenario can then be constructed. The sensitivity table not only provides a good test of the robustness of our results but also provides great insight into the value drivers in the firm, that is, which variables have the most impact on the firm’s bottom line.
The following provides the derivations of these sensitivity measures for a European option without dividend payments. In actual options analysis, it might be easier to compute the sensitivities based on a percentage change to each input rather than instantaneous changes. Nonetheless, these Greeks are useful when modeling simultaneous hedging strategies (e.g., gamma and delta-gamma hedges as described previously in this book).
Call Delta
Starting from ![]()
where
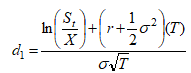 and
and![]()
we can get the call Delta, defined as the change in call value for a change in the underlying asset value, that is, the partial derivative![]() at an instantaneous time t. Differentiating, we obtain:
at an instantaneous time t. Differentiating, we obtain:
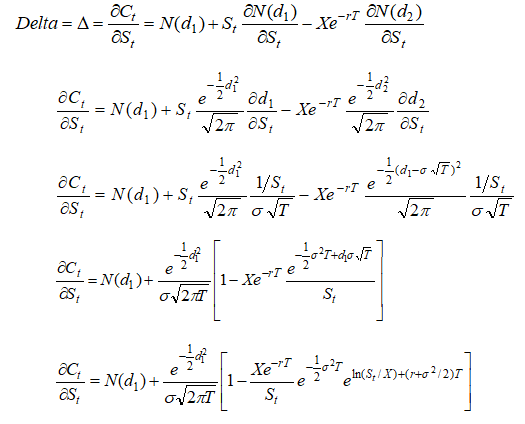
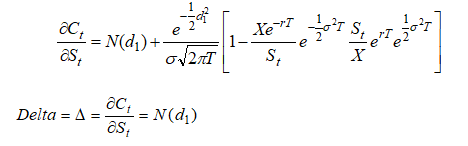
Call Gamma
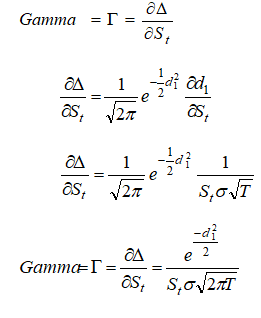
Call Rho
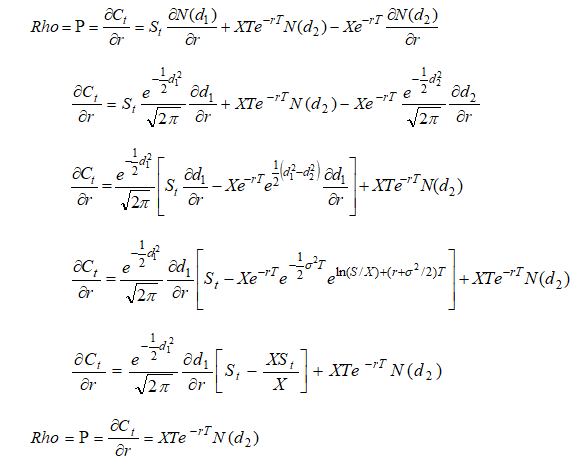
Call Theta
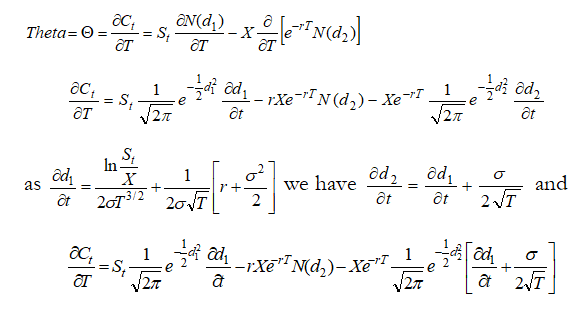
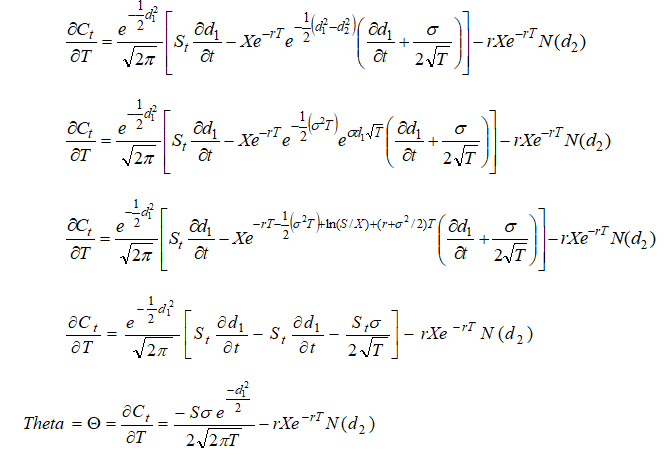
Call Vega
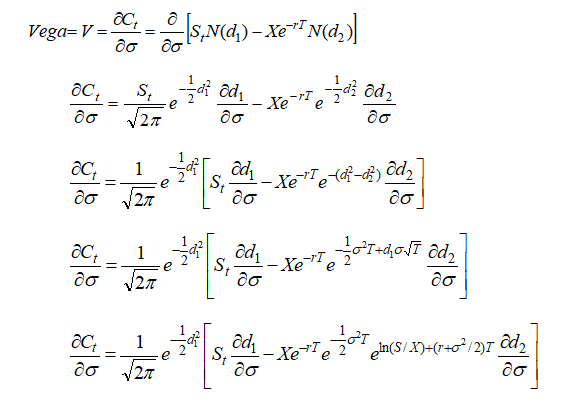
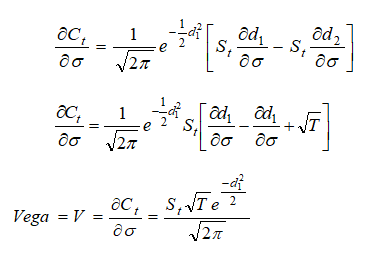
Call Xi