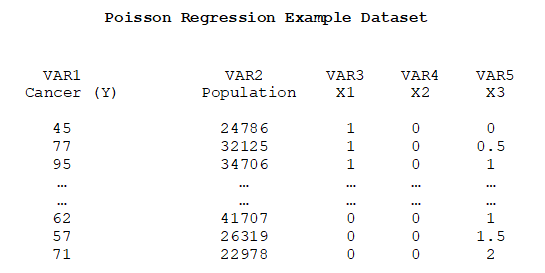
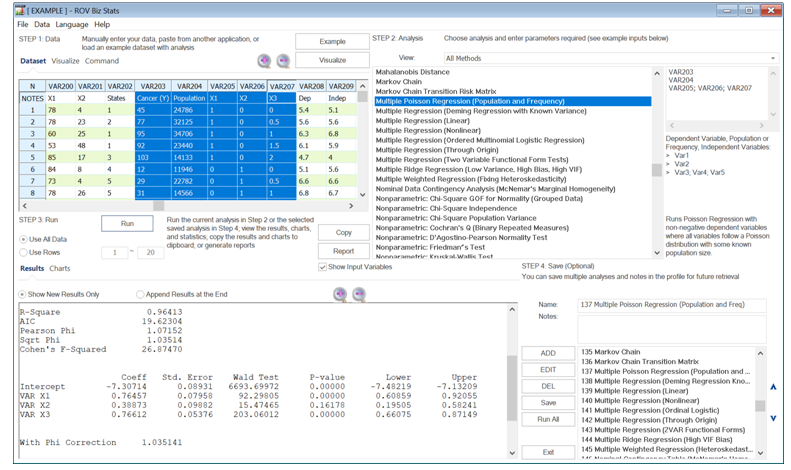
The Poisson regression is like the Logit regression in that the dependent variable can only take on non-negative values, but also that the underlying distribution of the data is a Poisson distribution, drawn from a known population size. Recall that the Poisson distribution is a discrete distribution used to model the probability that an event occurs within the context of time and area. Typically, this generalized linear model approach runs a log-linear regression model, where the dependent variable is the event count (see VAR1 in the sample dataset below), and an additional variable for the population size (VAR2) and categorical independent variables (VAR3 to VAR5) are needed.
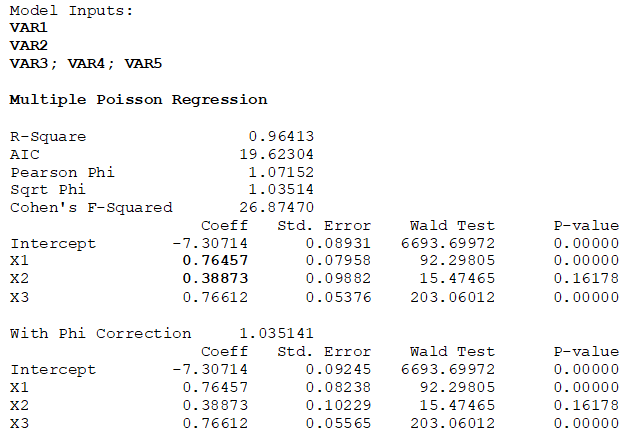
In Poisson regression, the logarithm of the expected value is a linear combination of the independent variables, that is, 
In the sample results below, we can say that the coefficient for
which is the expected log count of each unit increase in 
. Alternatively, 
which means that there is a 114.8% (a 2.148-fold) increase in Y for every unit increase in 
. Similarly,
has an expected log count of
which means that there is a 47.5% (a 1.475-fold) increase in for every unit increase in 
In addition, the interpretation of the p-values, R-square, and Akaike Information Criterion (AIC) are the same as a regular multiple regression. The new goodness-of-fit and error measures, such as Pearson’s Phi and Cohen’s F-Squared, test the null hypothesis that the current model is a good fit (null hypothesis states that the error is zero), which means we want these error measures to be small. These measures are typically used to compare against running other Poisson regression models, where a model with lower Pearson’s Phi, F-squared, and AIC indicates a better fit. R-square is an absolute measure in the sense that it has a fixed domain between 0 and 1 and can be readily interpreted (the percent variation in the dependent variable that can be explained by the variation in the independent variable). However, these other goodness-of-fit error measures like Phi, F-squared, and AIC are relative measures, where there is little interpretation by themselves, and are only used when comparing across multiple models.
